PSYC122-w17-how-to

Author

Rob Davies

Introduction

In Week 17, we aim to further develop skills in visualizing and testing the associations between variables in psychological data.

We do this to learn how to answer research questions like:

What person attributes predict success in understanding?
Can people accurately evaluate whether they correctly understand written health information?

These kinds of research questions can be answered using methods like the linear model.

When we do these analyses, we need to think about how we report the results:

we usually need to report information about the kind of model we specify;
and we will need to report the nature of the association estimated in our model;
we usually need to decide, is the association significant?
does the association reflect a positive or negative relationship between outcome and predictor?
and is the association we see in our sample data relatively strong or weak?

We will consolidate and extend learning on data visualization:

focusing on how we edit ggplot() code to produce professional looking plots.

Naming things

I will format dataset names like this:

study-one-general-participants.csv

I will also format variable (data column) names like this: variable

I will also format value or other data object (e.g. cell value) names like this: studyone

I will format functions and library names like this: e.g. function ggplot() or e.g. library {tidyverse}.

The data we will be using

In this activity, we use data from a 2020 study of the response of adults from a UK national sample to written health information:

study-one-general-participants.csv

Step 1: Set-up

To begin, we set up our environment in R.

Task 1 – Run code to empty the R environment

rm(list=ls())

Task 2 – Run code to load relevant libraries

library("tidyverse")

Warning: package 'tidyr' was built under R version 4.1.1

Warning: package 'purrr' was built under R version 4.1.1

Warning: package 'stringr' was built under R version 4.1.1

── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr     1.1.4     ✔ readr     2.1.4
✔ forcats   1.0.0     ✔ stringr   1.5.0
✔ ggplot2   3.5.1     ✔ tibble    3.2.1
✔ lubridate 1.9.2     ✔ tidyr     1.3.0
✔ purrr     1.0.1     
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

Step 2: Load the data

Task 3 – Read in the data file we will be using

The data file is called:

study-one-general-participants.csv

Use the read_csv() function to read the data file into R:

study.one.gen <- read_csv("study-one-general-participants.csv")

Rows: 169 Columns: 12
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (5): participant_ID, study, GENDER, EDUCATION, ETHNICITY
dbl (7): mean.acc, mean.self, AGE, SHIPLEY, HLVA, FACTOR3, QRITOTAL

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

When you read the data file in, give the data object you create a distinct name e.g. study.one.gen.

Task 4 – Inspect the data file

Use the summary() or head() functions to take a look.

head(study.one.gen)

# A tibble: 6 × 12
  participant_ID mean.acc mean.self study     AGE SHIPLEY  HLVA FACTOR3 QRITOTAL
  <chr>             <dbl>     <dbl> <chr>   <dbl>   <dbl> <dbl>   <dbl>    <dbl>
1 studyone.1         0.49      7.96 studyo…    34      33     7      53       11
2 studyone.10        0.85      7.28 studyo…    25      33     7      60       11
3 studyone.100       0.82      7.36 studyo…    43      40     8      46       12
4 studyone.101       0.94      7.88 studyo…    46      33    11      51       15
5 studyone.102       0.58      6.96 studyo…    18      32     3      51       12
6 studyone.103       0.84      7.88 studyo…    19      37    13      45       19
# ℹ 3 more variables: GENDER <chr>, EDUCATION <chr>, ETHNICITY <chr>

summary(study.one.gen)

 participant_ID        mean.acc        mean.self        study          
 Length:169         Min.   :0.3600   Min.   :3.440   Length:169        
 Class :character   1st Qu.:0.7600   1st Qu.:6.080   Class :character  
 Mode  :character   Median :0.8400   Median :7.080   Mode  :character  
                    Mean   :0.8163   Mean   :6.906                     
                    3rd Qu.:0.9000   3rd Qu.:7.920                     
                    Max.   :0.9900   Max.   :9.000                     
      AGE           SHIPLEY           HLVA           FACTOR3     
 Min.   :18.00   Min.   :23.00   Min.   : 3.000   Min.   :34.00  
 1st Qu.:24.00   1st Qu.:33.00   1st Qu.: 7.000   1st Qu.:46.00  
 Median :32.00   Median :35.00   Median : 9.000   Median :51.00  
 Mean   :34.87   Mean   :34.96   Mean   : 8.905   Mean   :50.33  
 3rd Qu.:42.00   3rd Qu.:38.00   3rd Qu.:10.000   3rd Qu.:55.00  
 Max.   :76.00   Max.   :40.00   Max.   :14.000   Max.   :63.00  
    QRITOTAL        GENDER           EDUCATION          ETHNICITY        
 Min.   : 6.00   Length:169         Length:169         Length:169        
 1st Qu.:12.00   Class :character   Class :character   Class :character  
 Median :13.00   Mode  :character   Mode  :character   Mode  :character  
 Mean   :13.36                                                           
 3rd Qu.:15.00                                                           
 Max.   :19.00

Notice that:

head() will give you the top few rows of any dataset you have read into R.
summary() will give you either descriptive statistics for variable columns classified as numeric or will tell you that columns in the dataset are not numeric.

Pay attention to what you see, for the numeric variables, in the information about minimum (Min.) and maximum (Max.) values. You will use this informatio later when you engage in data visualization.

Step 3: Use histograms to examine the distributions of variables

Revise: practice to strengthen skills

Task 5 – Draw histograms to examine the distributions of variables

hint: Task 5

Use ggplot() with geom_histogram().

When we create a plot, we take things step-by-step.

Here’s an example you have seen before: run the lines of code and see the result in the Plots window in R-Studio.

ggplot(data = study.one.gen, aes(x = mean.acc)) + 
  geom_histogram()

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.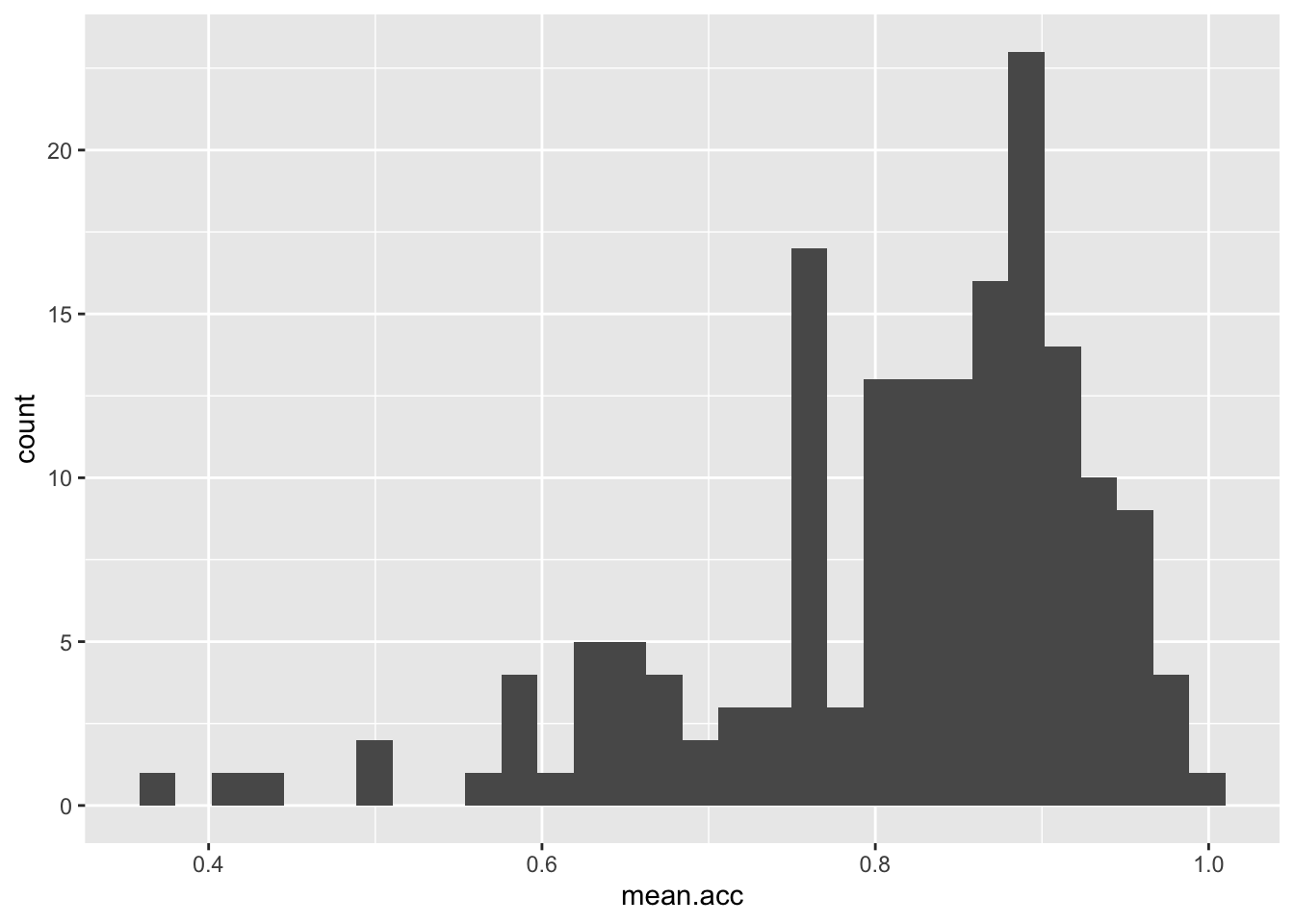

These are the steps, set out one at a time:

ggplot(...) you tell R you want to make a plot using the ggplot() function
ggplot(data = study.one.gen ...) you tell R you want to make a plot with the study.two.gen data
ggplot(..., aes(x = mean.acc)) you tell R that you want to make a plot with the variable mean.acc – here, you specify the aesthetic mapping, x = mean.acc
ggplot(...) + geom_histogram() you tell R you want to plot values of mean.acc as a histogram

Notice that the code works the same whether we have the different bits of code on the same line or in a series of lines.

Revise: make sure you are confident about doing these things

Task 6 – Practice editing the appearance of a histogram plot step-by-step

We are going to revise editing:

The appearance of the bars using binwidth;
The colour of the background using theme_bw();
The appearance of the labels using labs().

We proceed to revise:

Task 6.1 – the appearance of the bars using `binwidth`:

ggplot(data = study.one.gen, aes(x = SHIPLEY)) + 
  geom_histogram(binwidth = 2)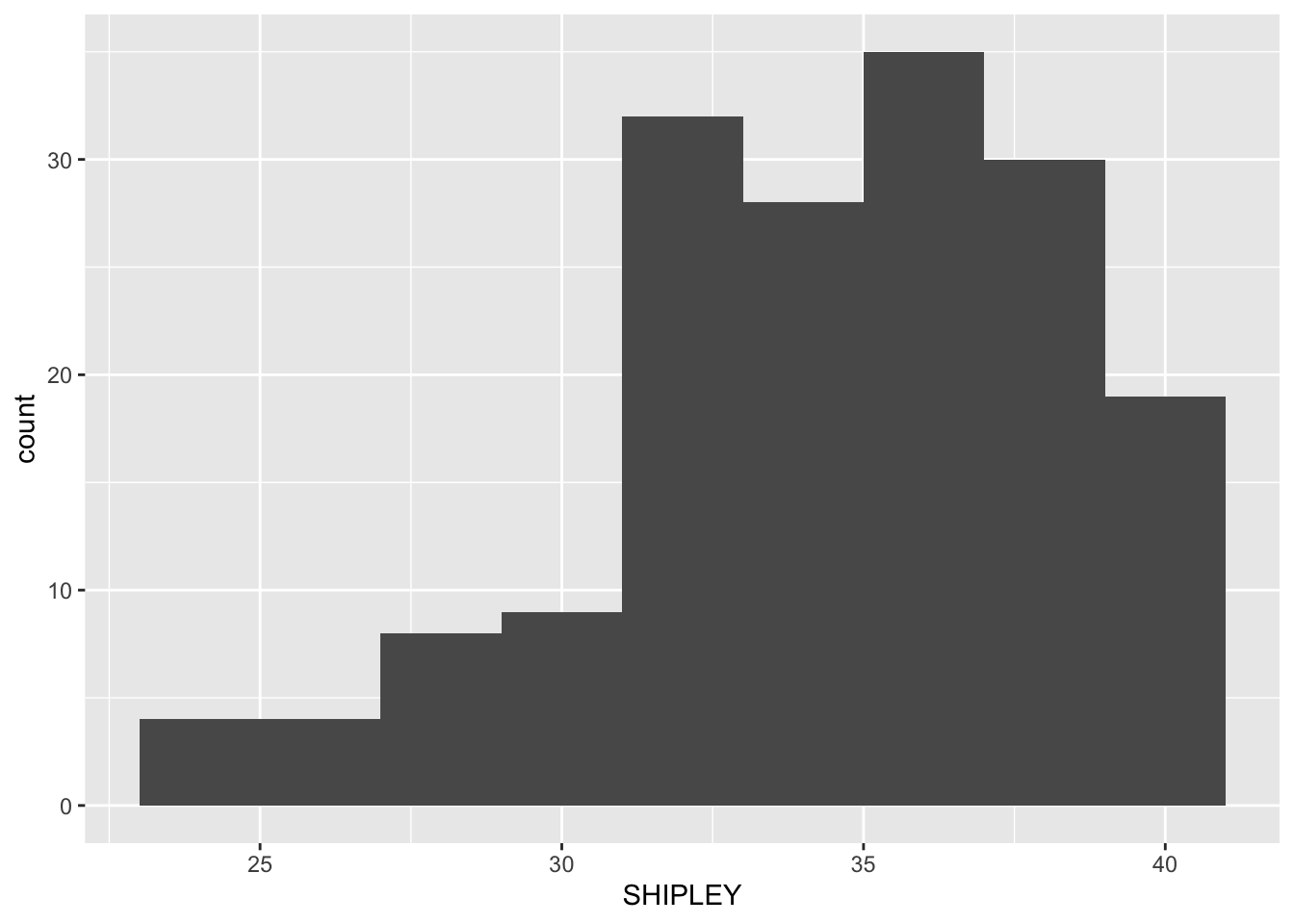

Task 6.2 – then the colour of the background using `theme_bw()`:

ggplot(data = study.one.gen, aes(x = SHIPLEY)) + 
  geom_histogram(binwidth = 2) +
  theme_bw()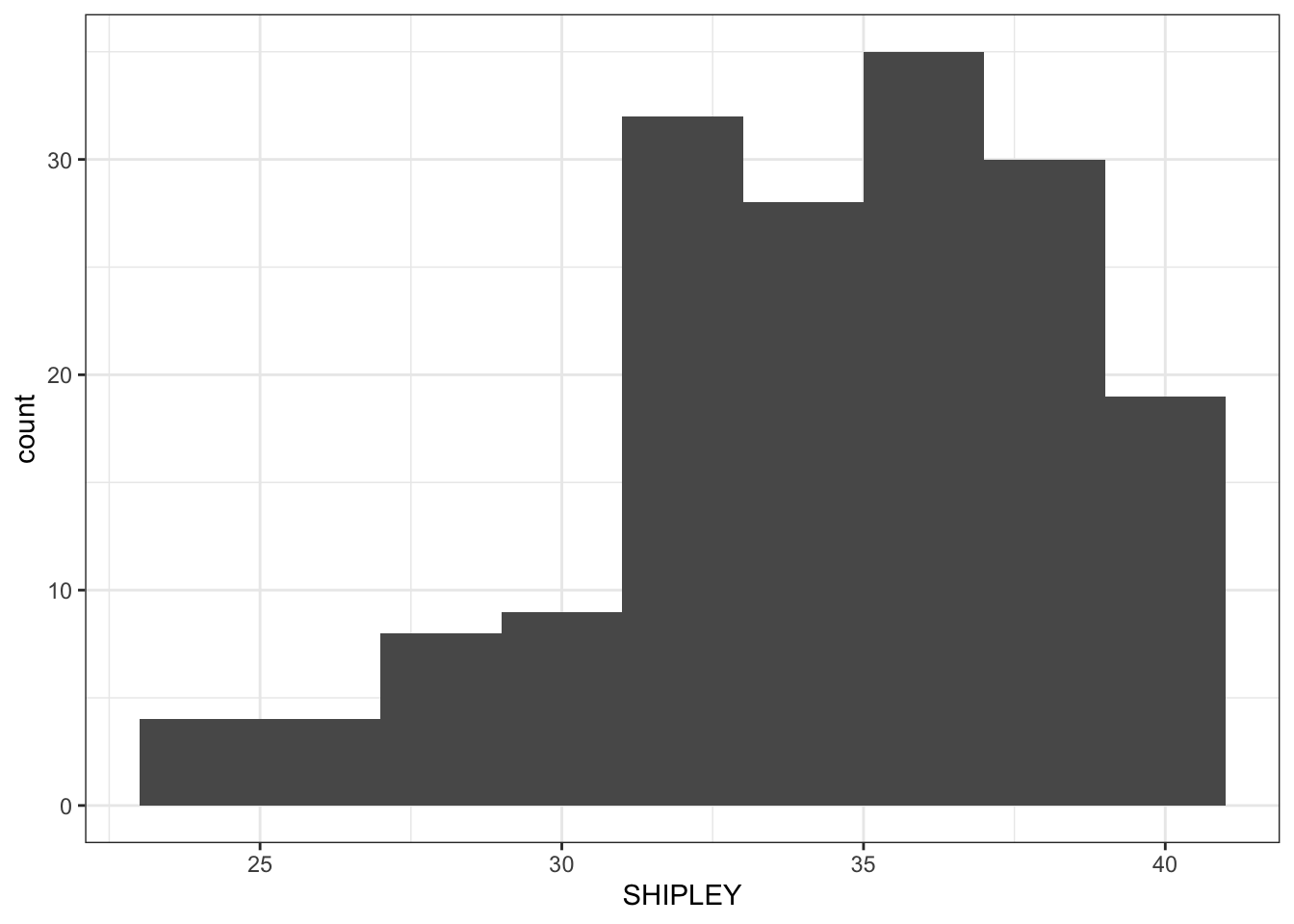

Task 6.3 – then the appearance of the labels using `labs()`:

ggplot(data = study.one.gen, aes(x = SHIPLEY)) + 
  geom_histogram(binwidth = 2) +
  theme_bw() +
  labs(x = "mean accuracy", y = "frequency count")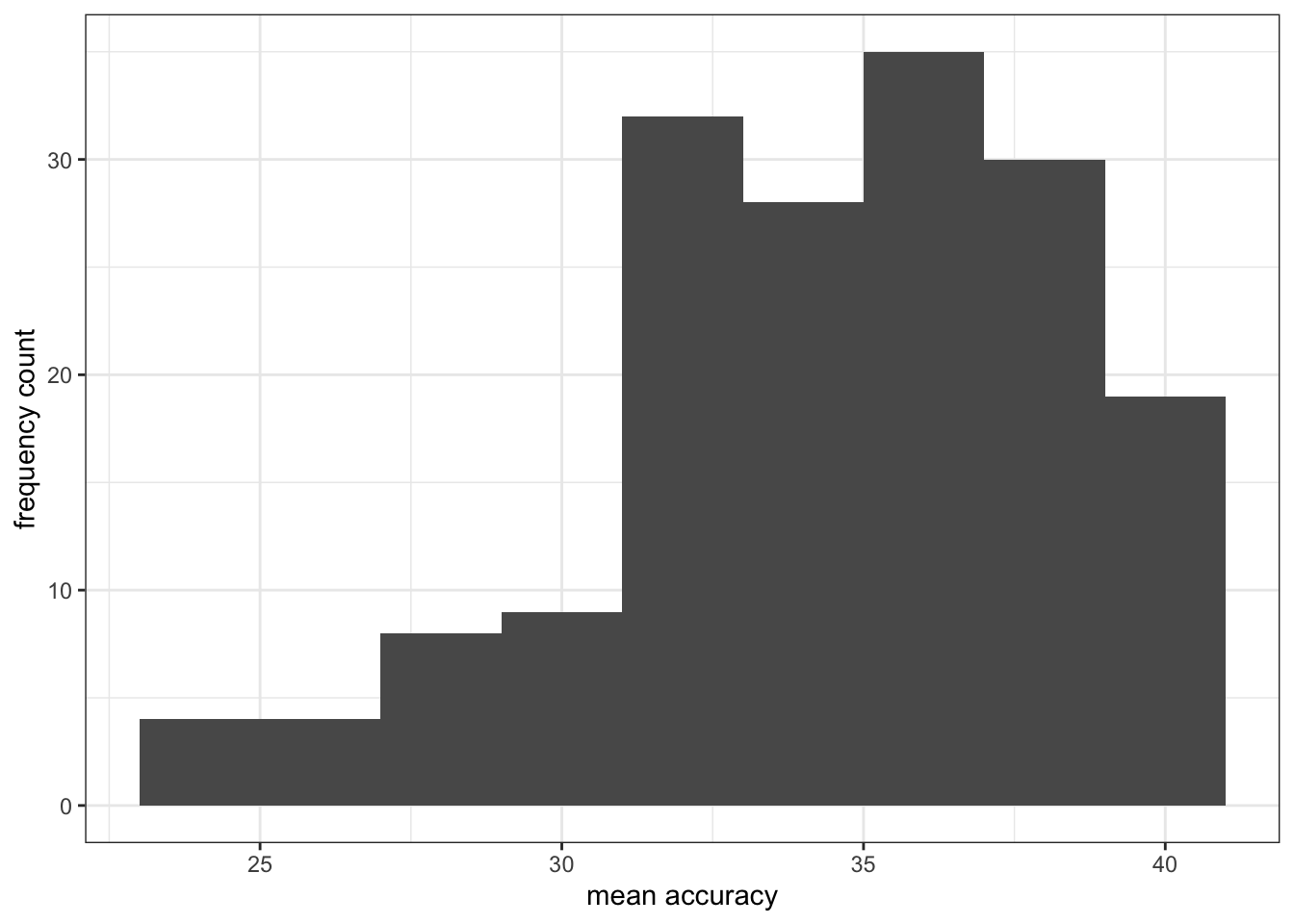

Introduce: make some new moves

Task 6.4. Now add an edit by setting the x-axis limits using `x.lim()`:

ggplot(data = study.one.gen, aes(x = SHIPLEY)) + 
  geom_histogram(binwidth = 2) +
  theme_bw() +
  labs(x = "Vocabulary (SHIPLEY)", y = "frequency count") +
  xlim(0,40)

Warning: Removed 2 rows containing missing values or values outside the scale range
(`geom_bar()`).

Task 6.5. Now add a vertical line to show the mean value:

ggplot(data = study.one.gen, aes(x = SHIPLEY)) + 
  geom_histogram(binwidth = 2) +
  theme_bw() +
  labs(x = "Vocabulary (SHIPLEY)", y = "frequency count") +
  xlim(0,40) +
  geom_vline(xintercept = mean(study.one.gen$SHIPLEY), colour = "red", size = 1.5)

Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
ℹ Please use `linewidth` instead.

Warning: Removed 2 rows containing missing values or values outside the scale range
(`geom_bar()`).

Why are we learning how to do this?

It is often useful to define the limits on the x-axis and on the y-axis:

Because we want to show the audience where the sample values are distributed compared to where they could be distributed, given the measure.
This makes sense e.g. if you want to see the relative age distribution of a sample compared to the population.
Because we want plots, shown side by side to be directly comparable.
And because we want to give the audience a more accurate picture of the data.

You can see ggplot reference information on setting limits here:

https://ggplot2.tidyverse.org/reference/lims.html

Notice that we used the geom_vline() in:

geom_vline(xintercept = mean(study.one.gen$SHIPLEY), colour = "red", size = 1.5)

to plot a vertical line at the location on the x-axis we define.

We do this in the steps:

geom_vline(...) draw a vertical line;
...xintercept... draw the line so it hits the x-axis (intercepts the x-axis);
...xintercept = mean(study.one.gen$SHIPLEY... defined by the mean of the variable mean(study.one.gen$SHIPLEY);
...colour = "red", size = 1.5... make the line red and make the line one and a half times thicker than the default line thickness.

See ggplot() reference information for this new geom is here:

https://ggplot2.tidyverse.org/reference/geom_abline.html

Step 4: Now draw scatterplots to examine associations between variables

Consolidation: should be no surprises here

Task 7 – Create a scatterplot to examine the association between some variables

hint: Task 7 – We are working with `geom_point()` and you need x and y aesthetic mappings.

hint: Task 7 – The outcome variable `mean.acc` has to be mapped to the y-axis using `...y = ...`

Run a chunk of code to make the plot.

ggplot(data = study.one.gen, aes(x = SHIPLEY, y = mean.acc)) +
  geom_point()

This plot shows:

the possible association between x-axis variable SHIPLEY and y-axis variable mean.acc.

The plot code moves through the following steps:

ggplot(...) make a plot;
ggplot(data = study.one.gen, ...) with the study.one.gen dataset;
ggplot(...aes(x = SHIPLEY, y = mean.acc)) using two aesthetic mappings

x = SHIPLEY map SHIPLEY values to x-axis (horizontal, left to right) positions;
y = mean.acc map mean.acc values to y-axis (vertical, bottom to top) positions;

geom_point() show the mappings as points.

Revise: make sure you are confident about doing these things

Task 8 – Edit the appearance of each plot step-by-step

We are going to revise making edits to:

the appearance of the points using alpha, size, shape, and colour;
the colour of the background using theme_bw();
the appearance of the labels using labs().

We are then going to try out some new moves:

Set the x-axis and y-axis limits to the potential minimum-maximum ranges of the variables we plot.

Here, “potential” references the fact that e.g. SHIPLEY scores can start at 0 (a person gets 0 responses correct) and has a maximum of 40 (a person could get all responses correct, for up to 40 items).

Task 8.1. Edit the appearance of the points using `alpha`, `size`, `shape`, and `colour`:

ggplot(data = study.one.gen, aes(x = SHIPLEY, y = mean.acc)) +
  geom_point(alpha = 0.5, size = 2, colour = "blue", shape = "square")

Task 8.2. Edit the colour of the background using `theme_bw()`:

ggplot(data = study.one.gen, aes(x = SHIPLEY, y = mean.acc)) +
  geom_point(alpha = 0.5, size = 2, colour = "blue", shape = "square")   +
  theme_bw()

Task 8.3. Edit the appearance of the labels using `labs()`:

ggplot(data = study.one.gen, aes(x = SHIPLEY, y = mean.acc)) +
  geom_point(alpha = 0.5, size = 2, colour = "blue", shape = "square")   +
  theme_bw() +
  labs(x = "SHIPLEY", y = "mean accuracy")

Introduce: make some new moves

Task 8.4. Set the axis limits:

ggplot(data = study.one.gen, aes(x = SHIPLEY, y = mean.acc)) +
  geom_point(alpha = 0.5, size = 2, colour = "blue", shape = "square")   +
  theme_bw() +
  labs(x = "SHIPLEY", y = "mean accuracy") +
  xlim(0, 40) + ylim(0, 1)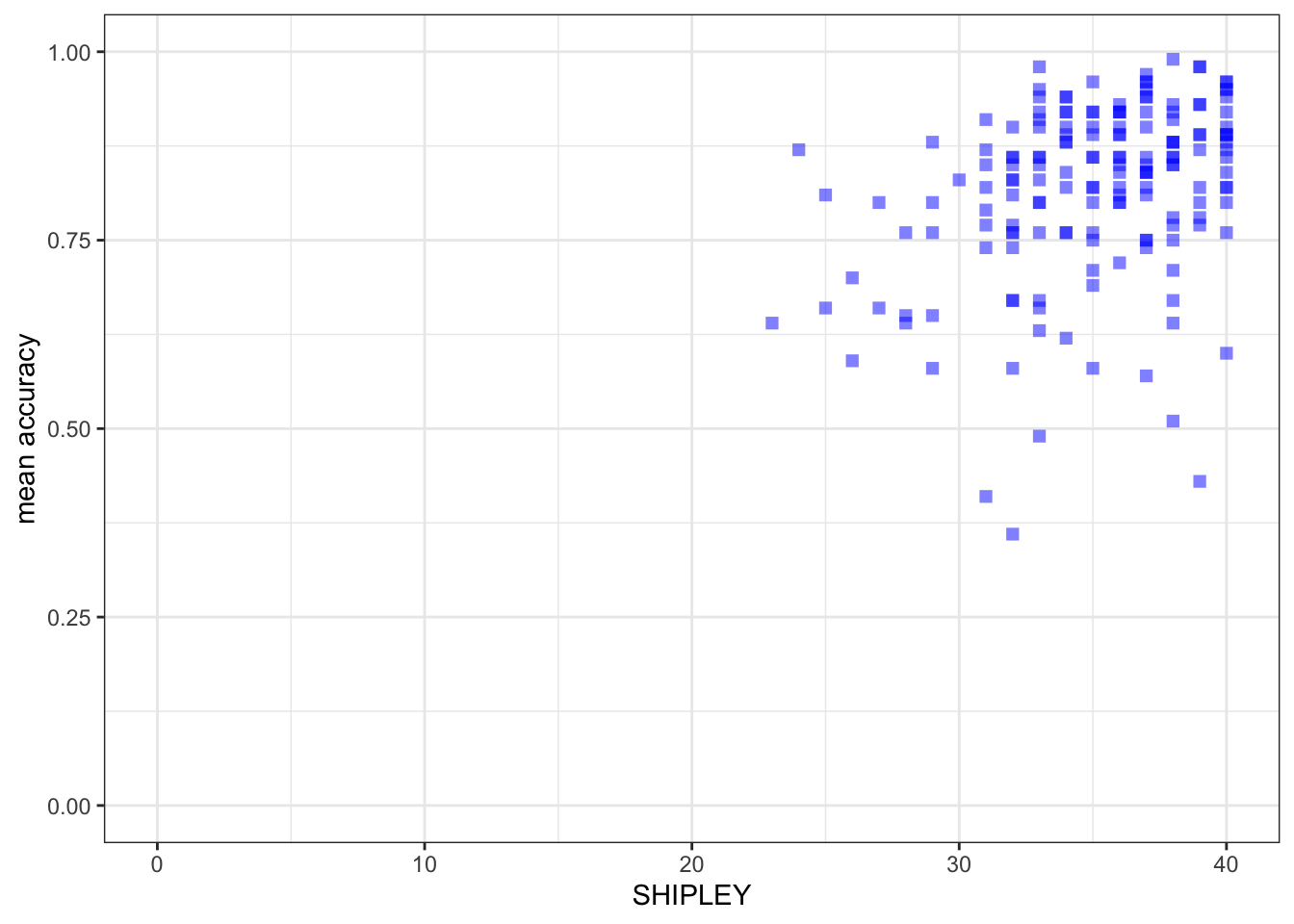

Notice that I set the x-axis limits to the minimum (0) and maximum (40) possible values for the SHIPLEY variable. - I set the y-axis limits to the minimum (0) and maximum (1) possible values for the mean accuracy variable mean.acc.

Why are we learning how to do this?

It is generally a good idea to show the minimum value (the origin) for each variable. Not doing this i.e. showing a more narrow slice of the sample range is an easy way to exaggerate the strength of associations or to imply incorrectly the breadth in variation.

You can change the transparency (alpha), size, colour and shape of important parts of a plot.

Here, we are changing the appearance of the points.
But you can also change the transparency (alpha), size, colour and shape of reference lines added to a plot.

The ggplot geom_point()reference information is here:

https://ggplot2.tidyverse.org/reference/geom_point.html

where you can see some examples of the edits we have done.

Some useful information about shape options is here:

http://www.cookbook-r.com/Graphs/Shapes_and_line_types/

Some useful information about colourons is here:

http://www.cookbook-r.com/Graphs/Colors_(ggplot2)/

Now experiment!

Step 5: Use a linear model to to answer the research questions

Introduce: Make some new moves

One of our research questions is:

What person attributes predict success in understanding?

Task 9 – Examine the relation between outcome mean accuracy (`mean.acc`) and the predictor variable: vocabulary (`SHIPLEY`)

hint: Task 9 – We use `lm()`

Fit the model and get a summary of the model statistics.

model <- lm(mean.acc ~ SHIPLEY, data = study.one.gen)
summary(model)


Call:
lm(formula = mean.acc ~ SHIPLEY, data = study.one.gen)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.42871 -0.04921  0.02079  0.07480  0.18430 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.44914    0.08053   5.577 9.67e-08 ***
SHIPLEY      0.01050    0.00229   4.585 8.85e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1115 on 167 degrees of freedom
Multiple R-squared:  0.1118,    Adjusted R-squared:  0.1065 
F-statistic: 21.03 on 1 and 167 DF,  p-value: 8.846e-06

Notice that we do the linear model in the steps:

model <- lm(...) fit the model using lm(...), give the model a name – here, we call it “model”;
...lm(mean.acc ~ SHIPLEY...) tell R you want a model of the outcome mean.acc predicted (~) by the predictor SHIPLEY;
...data = study.one.gen) tell R that the variables you name in the formula live in the study.one.gen dataset;
summary(model) ask R for a summary of the model you called “model”.

Notice: R has a general formula syntax: outcome ~ predictor or y ~ x

and uses the same format across a number of different functions;
each time, the left of the tilde symbol ~ is some output or outcome;
and the right of the tilde ~ is some input or predictor or set of predictors.

Questions: Task 9

If you look at the model summary you can answer the following questions.

Q.5. What is the estimate for the coefficient of the effect of the predictor, SHIPLEY?
A.5. 0.01050
Q.6. Is the effect significant?
A.6. It is significant, p < .05
Q.7. What are the values for t and p for the significance test for the coefficient?
A.7. t = 4.585, p = 8.85e-06
Q.8. What do you conclude is the answer to the research question, given the linear model results?
A.8. The model slope estimate suggests that as SHIPLEY scores increase so mean.acc scores increase also.

Step 6: Use a linear model to generate predictions

Introduce: make some new moves

Task 10 – We can use the model we have just fitted to plot the model predictions

hint: Task 10 – We are going to draw a scatterplot and add a line

The line will show the model predictions, given the model intercept and effect coefficient estimates.

First fit a model and get a summary: model the relationship between mean.acc and SHIPLEY

model <- lm(mean.acc ~ SHIPLEY, data = study.one.gen)
summary(model)


Call:
lm(formula = mean.acc ~ SHIPLEY, data = study.one.gen)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.42871 -0.04921  0.02079  0.07480  0.18430 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.44914    0.08053   5.577 9.67e-08 ***
SHIPLEY      0.01050    0.00229   4.585 8.85e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1115 on 167 degrees of freedom
Multiple R-squared:  0.1118,    Adjusted R-squared:  0.1065 
F-statistic: 21.03 on 1 and 167 DF,  p-value: 8.846e-06

Q.9. What is the coefficient estimate for the intercept?
A.9. 0.44914
Q.10. What is the coefficient estimate for the slope of SHIPLEY?
A.10. 0.01050

Second, use the geom_abline() function to draw the line:

ggplot(data = study.one.gen, aes(x = SHIPLEY, y = mean.acc)) +
  geom_point(alpha = 0.5, size = 2, colour = "blue", shape = "square")   +
  geom_abline(intercept = 0.44914, slope = 0.01050, colour = "red", size = 1.5) +
  theme_bw() +
  labs(x = "SHIPLEY", y = "mean accuracy") +
  xlim(0, 40) + ylim(0, 1)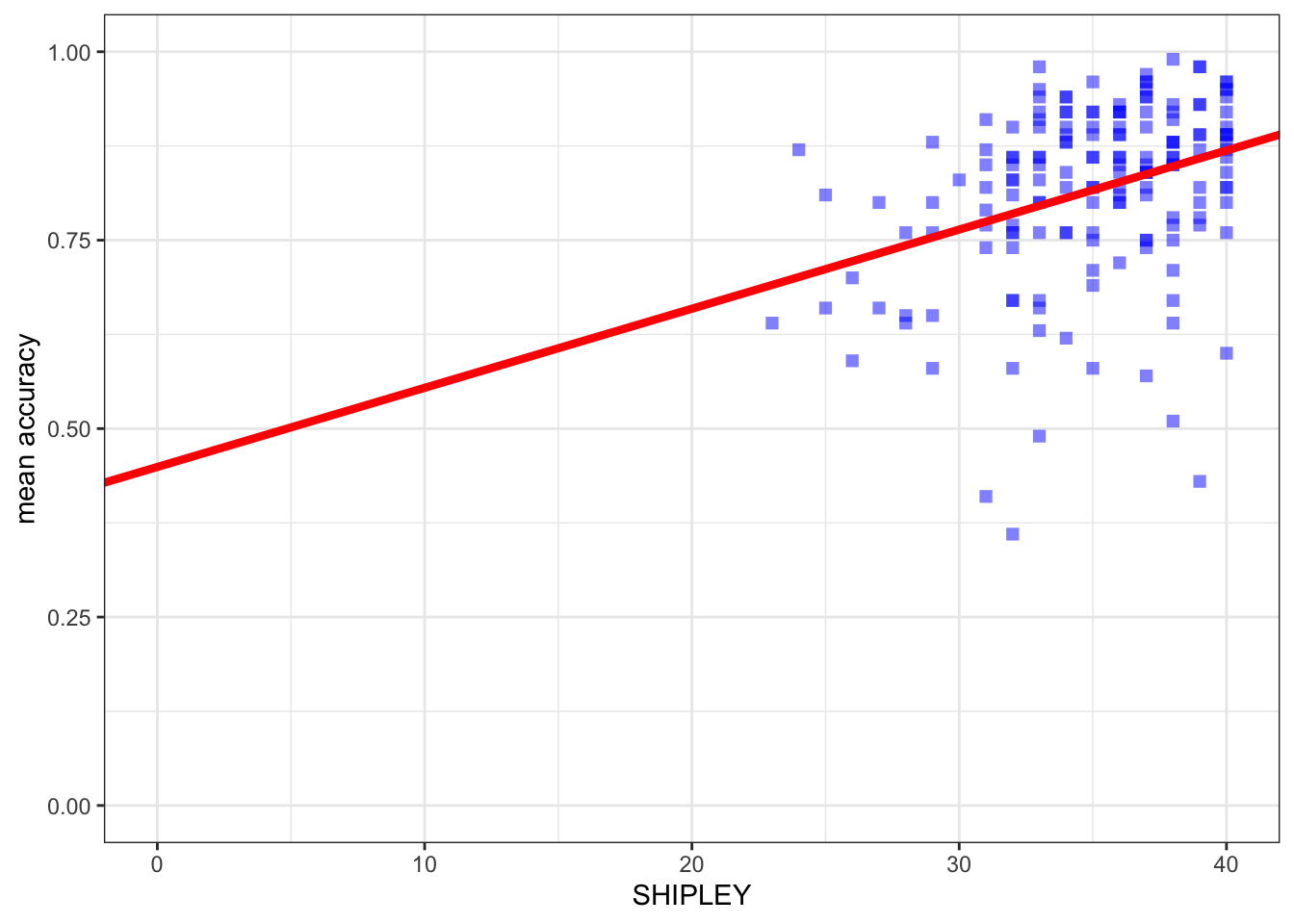

You can see that what we do is:

add the geom_abline(...) function;
and into that function code, we add information about the intercept and the slope which we take from the model summary.

You can see reference information here:

https://ggplot2.tidyverse.org/reference/geom_abline.html

Note that we can get the prediction line drawn for us automatically, as:

ggplot(data = study.one.gen, aes(x = SHIPLEY, y = mean.acc)) +
  # geom_point(alpha = 0.5, size = 2, colour = "blue", shape = `square`)   +
  geom_smooth(method = "lm", colour = "purple", alpha = .2, size = 2.5, se = FALSE) +
  geom_abline(intercept = 0.44914, slope = 0.01050, colour = "red", size = 1) +
  theme_bw() +
  labs(x = "SHIPLEY", y = "mean accuracy") +
  xlim(0, 40) + ylim(0, 1)

`geom_smooth()` using formula = 'y ~ x'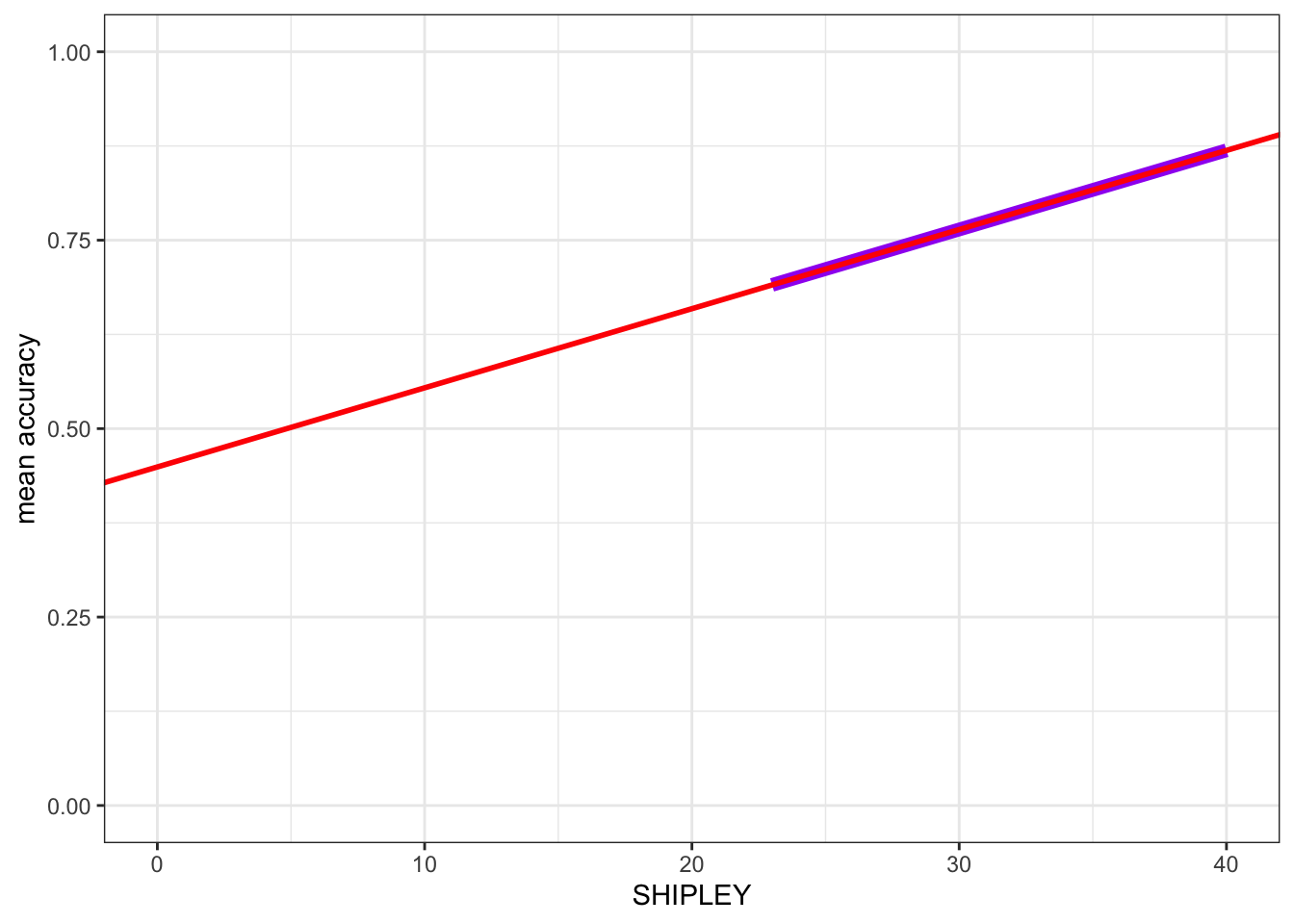

Here, I turned the points off by commenting them out, adding # to the start of the line.
And I added geom_smooth(method = "lm", ...) to draw a prediction line.
You can compare the red prediction line I drew using the model estimates
with the purple line I used geom_smooth() to draw automatically to see that they are identical

This shows you something of what geom_smooth() does. It is very useful:

https://ggplot2.tidyverse.org/reference/geom_smooth.html

Introduction

Naming things

The data we will be using

Step 1: Set-up

Task 1 – Run code to empty the R environment

Task 2 – Run code to load relevant libraries

Step 2: Load the data

Task 3 – Read in the data file we will be using

Task 4 – Inspect the data file

Step 3: Use histograms to examine the distributions of variables

Revise: practice to strengthen skills

Task 5 – Draw histograms to examine the distributions of variables

hint: Task 5

Revise: make sure you are confident about doing these things

Task 6 – Practice editing the appearance of a histogram plot step-by-step

Task 6.1 – the appearance of the bars using binwidth:

Task 6.2 – then the colour of the background using theme_bw():

Task 6.3 – then the appearance of the labels using labs():

Introduce: make some new moves

Task 6.4. Now add an edit by setting the x-axis limits using x.lim():

Task 6.5. Now add a vertical line to show the mean value:

Why are we learning how to do this?

Step 4: Now draw scatterplots to examine associations between variables

Consolidation: should be no surprises here

Task 7 – Create a scatterplot to examine the association between some variables

hint: Task 7 – We are working with geom_point() and you need x and y aesthetic mappings.

hint: Task 7 – The outcome variable mean.acc has to be mapped to the y-axis using ...y = ...

Revise: make sure you are confident about doing these things

Task 8 – Edit the appearance of each plot step-by-step

Task 8.1. Edit the appearance of the points using alpha, size, shape, and colour:

Task 8.2. Edit the colour of the background using theme_bw():

Task 8.3. Edit the appearance of the labels using labs():

Introduce: make some new moves

Task 8.4. Set the axis limits:

Why are we learning how to do this?

Now experiment!

Step 5: Use a linear model to to answer the research questions

Introduce: Make some new moves

Task 9 – Examine the relation between outcome mean accuracy (mean.acc) and the predictor variable: vocabulary (SHIPLEY)

hint: Task 9 – We use lm()

Questions: Task 9

Step 6: Use a linear model to generate predictions

Introduce: make some new moves

Task 10 – We can use the model we have just fitted to plot the model predictions

hint: Task 10 – We are going to draw a scatterplot and add a line

Task 6.1 – the appearance of the bars using `binwidth`:

Task 6.2 – then the colour of the background using `theme_bw()`:

Task 6.3 – then the appearance of the labels using `labs()`:

Task 6.4. Now add an edit by setting the x-axis limits using `x.lim()`:

hint: Task 7 – We are working with `geom_point()` and you need x and y aesthetic mappings.

hint: Task 7 – The outcome variable `mean.acc` has to be mapped to the y-axis using `...y = ...`

Task 8.1. Edit the appearance of the points using `alpha`, `size`, `shape`, and `colour`:

Task 8.2. Edit the colour of the background using `theme_bw()`:

Task 8.3. Edit the appearance of the labels using `labs()`:

Task 9 – Examine the relation between outcome mean accuracy (`mean.acc`) and the predictor variable: vocabulary (`SHIPLEY`)

hint: Task 9 – We use `lm()`