2023-24-PSYC122-w16-workbook-answers

Author

Rob Davies

Published

February 12, 2024

Introduction

In Week 16, we aim to develop skills in visualizing and testing the associations between variables in psychological data.

We do this to learn how to answer research questions like:

What person attributes predict success in understanding?
Can people accurately evaluate whether they correctly understand written health information?

These kinds of research questions can be answered using methods like correlation and linear models.

We will consolidate and extend learning on data visualization:

Use histograms to examine the distributions of variables;
Use scatterplots to examine the relationships we may observe or predict.

Naming things

I will format dataset names like this:

study-two-general-participants.csv

I will also format variable (data column) names like this: variable

I will also format value or other data object (e.g. cell value) names like this: studyone

I will format functions and library names like this: e.g. function ggplot() or e.g. library {tidyverse}.

The data we will be using

In this activity, we use data from a second 2020 study of the response of adults from a UK national sample to written health information:

study-two-general-participants.csv

Answers

Step 1: Set-up

To begin, we set up our environment in R.

Task 1 – Run code to empty the R environment

rm(list=ls())

Task 2 – Run code to load relevant libraries

library("tidyverse")

Warning: package 'tidyr' was built under R version 4.1.1

Warning: package 'purrr' was built under R version 4.1.1

Warning: package 'stringr' was built under R version 4.1.1

── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr     1.1.4     ✔ readr     2.1.4
✔ forcats   1.0.0     ✔ stringr   1.5.0
✔ ggplot2   3.4.4     ✔ tibble    3.2.1
✔ lubridate 1.9.2     ✔ tidyr     1.3.0
✔ purrr     1.0.1     
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

Step 2: Load the data

Task Task 3 – Read in the data file we will be using

The data file is called:

study-two-general-participants.csv

Use the read_csv() function to read the data file into R:

study.two.gen <- read_csv("study-two-general-participants.csv")

Rows: 172 Columns: 12
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (5): participant_ID, study, GENDER, EDUCATION, ETHNICITY
dbl (7): mean.acc, mean.self, AGE, SHIPLEY, HLVA, FACTOR3, QRITOTAL

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

When you read the data file in, give the data object you create a clear name e.g. study.two.gen.

Task 4 – Inspect the data file

Use the summary() or head() functions to take a look

summary(study.two.gen)

 participant_ID        mean.acc        mean.self        study          
 Length:172         Min.   :0.4107   Min.   :3.786   Length:172        
 Class :character   1st Qu.:0.6786   1st Qu.:6.411   Class :character  
 Mode  :character   Median :0.7679   Median :7.321   Mode  :character  
                    Mean   :0.7596   Mean   :7.101                     
                    3rd Qu.:0.8393   3rd Qu.:7.946                     
                    Max.   :0.9821   Max.   :9.000                     
      AGE           SHIPLEY           HLVA           FACTOR3     
 Min.   :18.00   Min.   :23.00   Min.   : 3.000   Min.   :29.00  
 1st Qu.:25.00   1st Qu.:32.75   1st Qu.: 7.750   1st Qu.:47.00  
 Median :32.50   Median :36.00   Median : 9.000   Median :51.00  
 Mean   :35.37   Mean   :35.13   Mean   : 9.064   Mean   :51.24  
 3rd Qu.:44.00   3rd Qu.:39.00   3rd Qu.:11.000   3rd Qu.:56.25  
 Max.   :76.00   Max.   :40.00   Max.   :14.000   Max.   :63.00  
    QRITOTAL        GENDER           EDUCATION          ETHNICITY        
 Min.   : 6.00   Length:172         Length:172         Length:172        
 1st Qu.:12.00   Class :character   Class :character   Class :character  
 Median :14.00   Mode  :character   Mode  :character   Mode  :character  
 Mean   :13.88                                                           
 3rd Qu.:16.00                                                           
 Max.   :20.00

Q.1. What is the median of AGE?
A.1. 32.50
Q.2. What class is the variable ETHNICITY?
A.2. character
Q.3. Does the summary indicate if any variable has missing values (NAs)?
Q.3. No

Task 5 – Change the class or type of the variable `ETHNICITY` to factor

You can use the as.factor() function you have used before:

study.two.gen$ETHNICITY <- as.factor(study.two.gen$ETHNICITY)

Q.4. After you have done this, what information does summary() give you about the variable ETHNICITY?

summary(study.two.gen)

 participant_ID        mean.acc        mean.self        study          
 Length:172         Min.   :0.4107   Min.   :3.786   Length:172        
 Class :character   1st Qu.:0.6786   1st Qu.:6.411   Class :character  
 Mode  :character   Median :0.7679   Median :7.321   Mode  :character  
                    Mean   :0.7596   Mean   :7.101                     
                    3rd Qu.:0.8393   3rd Qu.:7.946                     
                    Max.   :0.9821   Max.   :9.000                     
      AGE           SHIPLEY           HLVA           FACTOR3     
 Min.   :18.00   Min.   :23.00   Min.   : 3.000   Min.   :29.00  
 1st Qu.:25.00   1st Qu.:32.75   1st Qu.: 7.750   1st Qu.:47.00  
 Median :32.50   Median :36.00   Median : 9.000   Median :51.00  
 Mean   :35.37   Mean   :35.13   Mean   : 9.064   Mean   :51.24  
 3rd Qu.:44.00   3rd Qu.:39.00   3rd Qu.:11.000   3rd Qu.:56.25  
 Max.   :76.00   Max.   :40.00   Max.   :14.000   Max.   :63.00  
    QRITOTAL        GENDER           EDUCATION         ETHNICITY  
 Min.   : 6.00   Length:172         Length:172         Asian: 15  
 1st Qu.:12.00   Class :character   Class :character   Black:  5  
 Median :14.00   Mode  :character   Mode  :character   Mixed:  7  
 Mean   :13.88                                         White:145  
 3rd Qu.:16.00                                                    
 Max.   :20.00

A.4. We can see that ETHNICITY lists observations following UK Office National Statistics ethnicity grouping:
Asian: 15
Black: 5
Mixed: 7
White: 145

Step 3: Use histograms to examine the distributions of variables

Task 6 – Draw histograms to examine the distributions of variables

Hint: Task 6

Use ggplot() with geom_histogram().

The first time we do this, we take things step-by-step.

Here’s an example: run the line of code and see the result in the Plots window in R-Studio.

ggplot(data = study.two.gen, aes(x = mean.acc)) + geom_histogram()

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.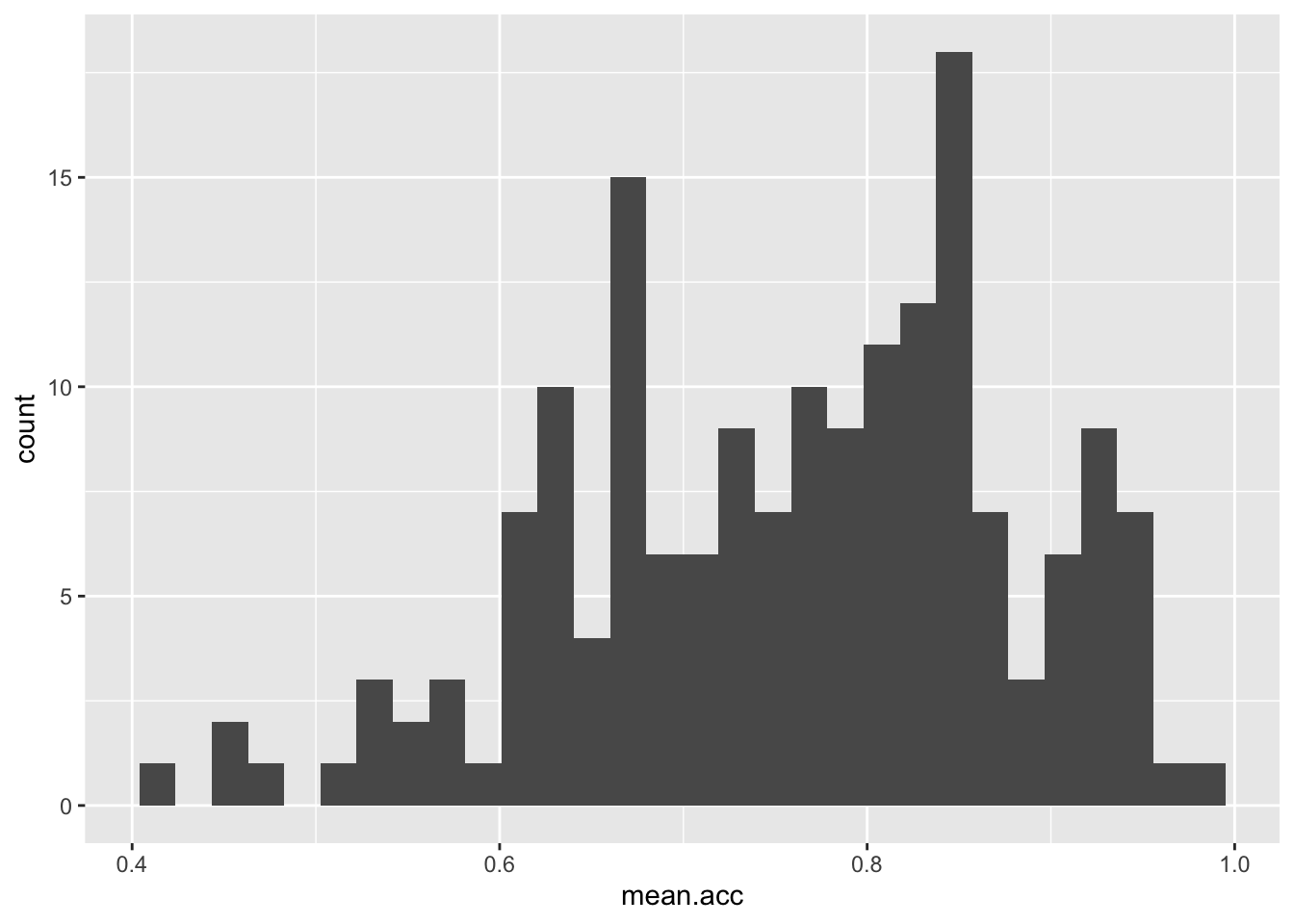

These are the steps, set out one at a time:

ggplot(...) you tell R you want to make a plot using the ggplot() function
ggplot(data = study.two.gen ...) you tell R you want to make a plot with the study.two.gen data
ggplot(..., aes(x = mean.acc)) you tell R that you want to make a plot with the variable mean.acc – here, you specify the aesthetic mapping, x = mean.acc
ggplot(...) + geom_histogram() you tell R you want to plot values of mean.acc as a histogram

Questions: Task 6

Q.5. Did you get a message in the Console window in R-Studio: what does it say?
A.5. The message says:
stat_bin() using bins = 30. Pick better value with binwidth.
Q.6. Draw two different histograms to examine the distributions of two different variables: SHIPLEY and HLVA

ggplot(data = study.two.gen, aes(x = SHIPLEY)) + geom_histogram()

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.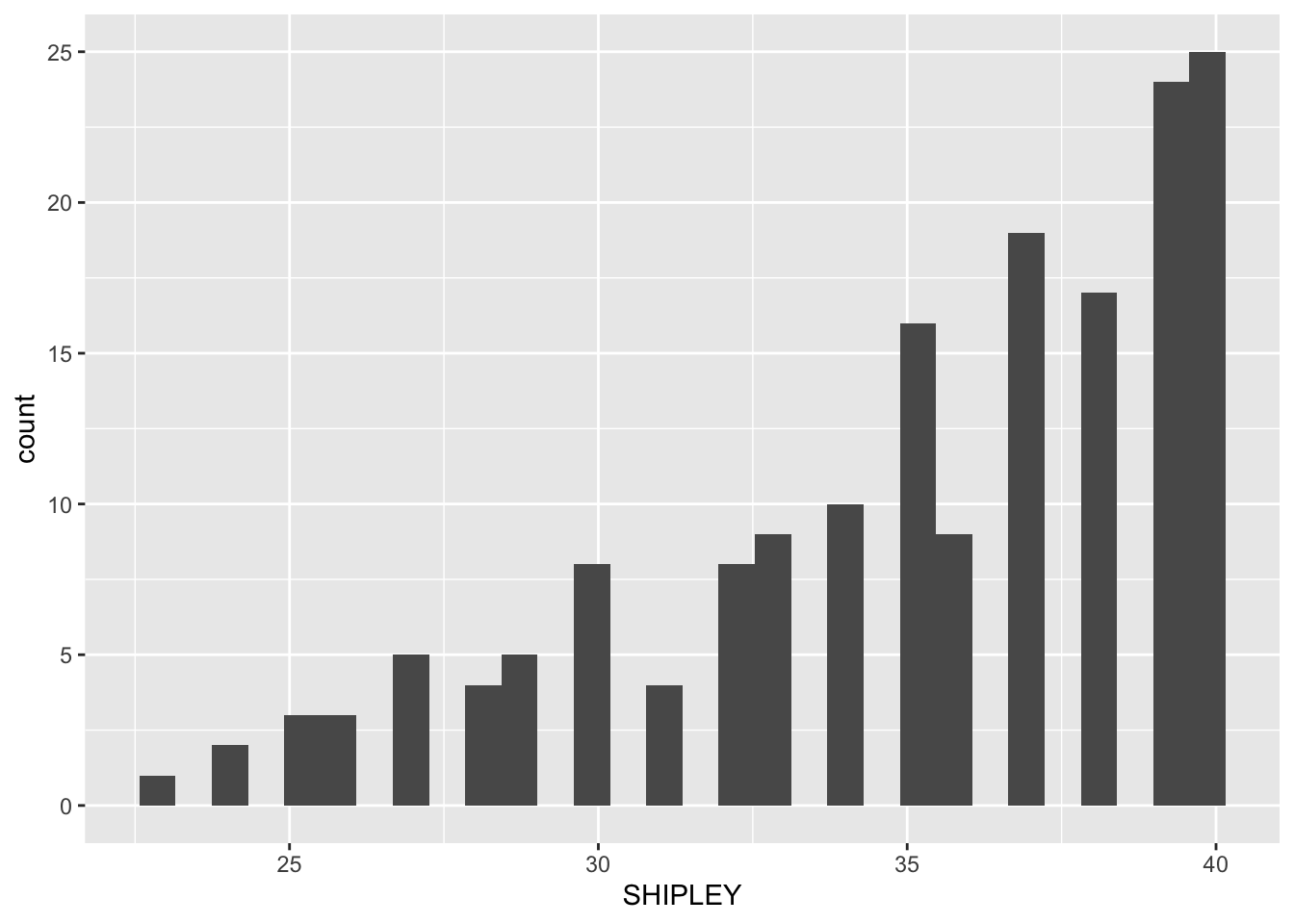

ggplot(data = study.two.gen, aes(x = HLVA)) + geom_histogram()

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.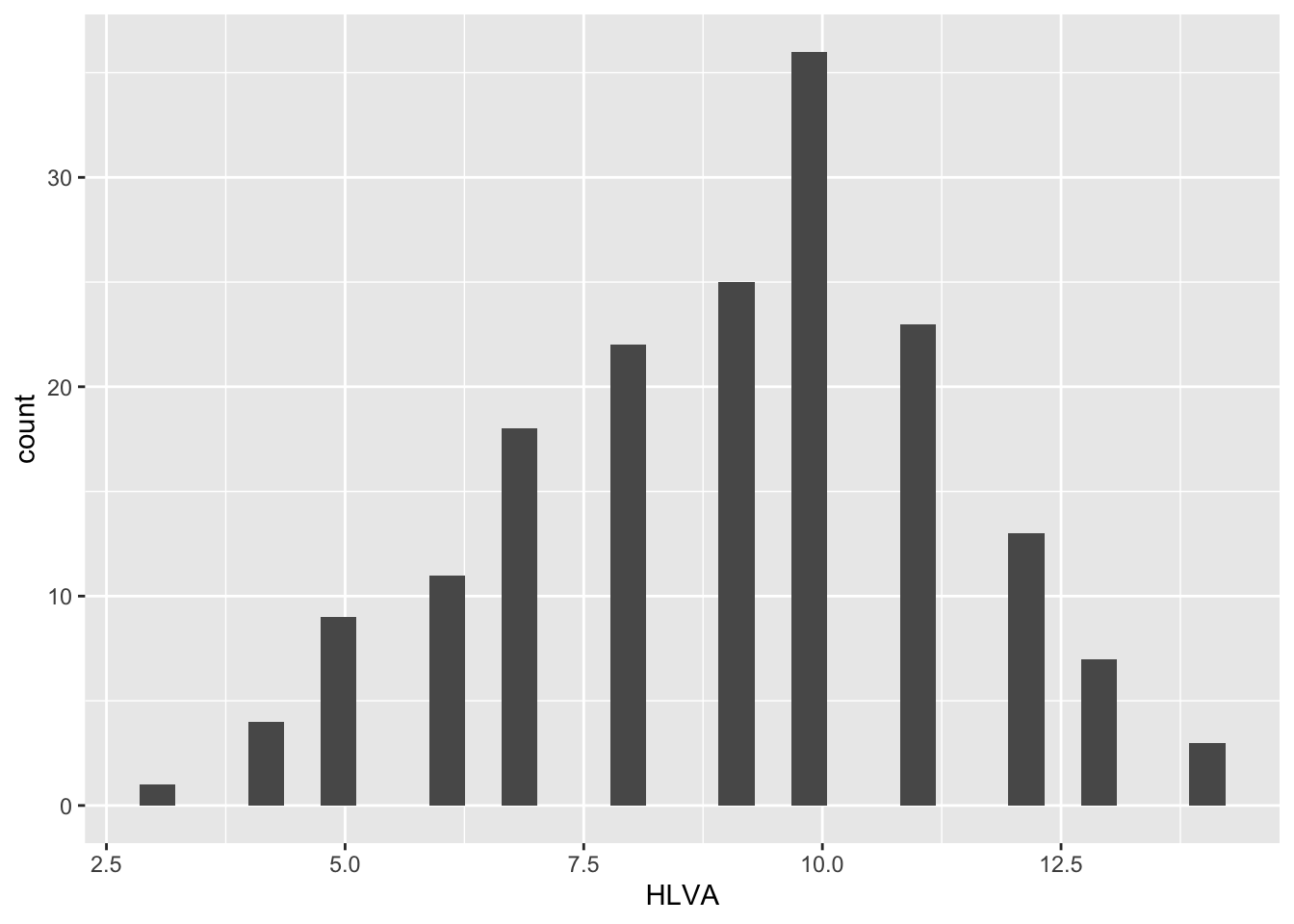

Q.7. Now re-do both plots: can you change the binwidth in geom_histogram() to make the bars wider?

If you are going to change binwidth the number you use needs to be a number larger than
the minimum and smaller than the maximum for the variable.

Remember, min and max values are given for each numeric variable in summary().

ggplot(data = study.two.gen, aes(x = SHIPLEY)) + geom_histogram(binwidth = 2)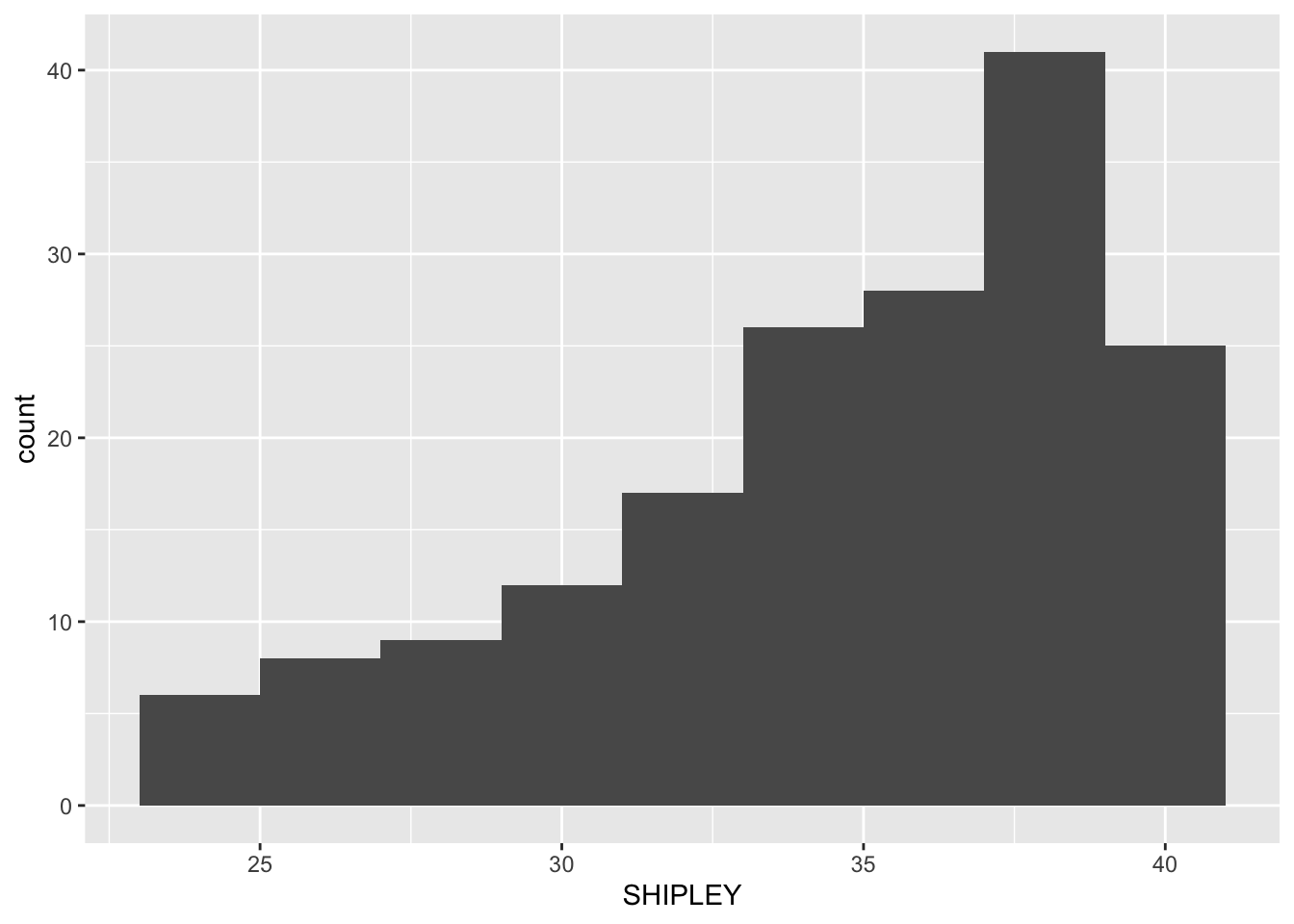

ggplot(data = study.two.gen, aes(x = HLVA)) + geom_histogram(binwidth = 2)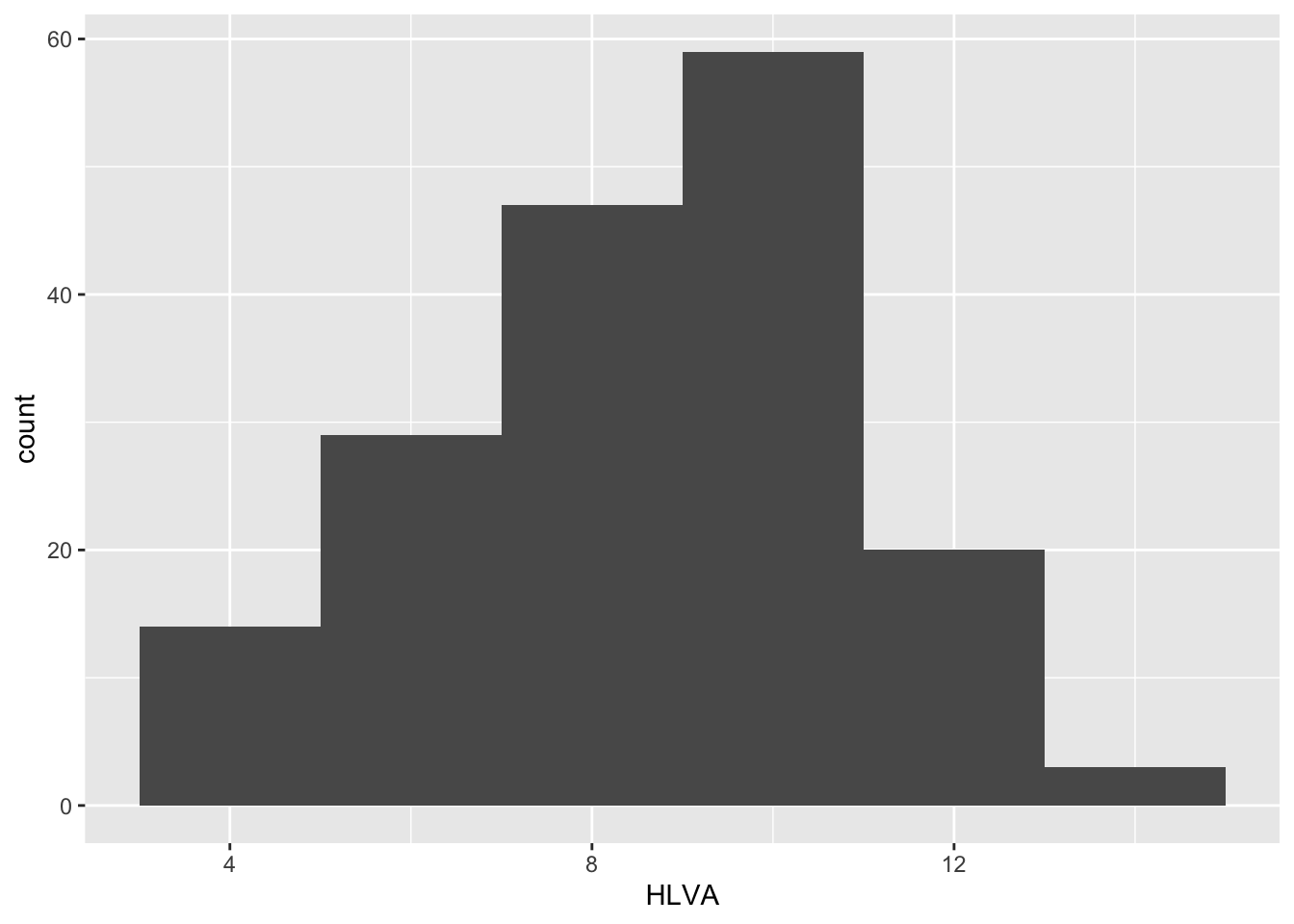

We adjust binwidth typically to improve the appearance of the plot.

This is a bit subjective so try different numbers and see how you feel about the changes in appearance.

We want histograms that show us enough detail about the frequency of occurrence of groupings (bins) of values for each variable.

But we do not want histograms that show us so much detail it is difficult to see the pattern for the distribution.

Q.8 – How would you describe the distributions – in a sentence – of the distributions of the SHIPLEY and HLVA variable values for our sample?
A.8. The SHIPLEY values lie between about 25 and 40, and are skewed towards high scores.
A.8. The HLVA values lie between 4 and about 14, and peak in the middle (near 7).

Step 4: Edit your plots to make them look good

Task 7 – Edit the appearance of a histogram plot for one numeric variable

Note that ggplot() code does not all have to be on the same line.

You can create a new plot for each edit so you can see what difference your edits make.

Q.9. Edit the appearance of the bars using binwidth

ggplot(data = study.two.gen, aes(x = HLVA)) + 
  geom_histogram(binwidth = 2)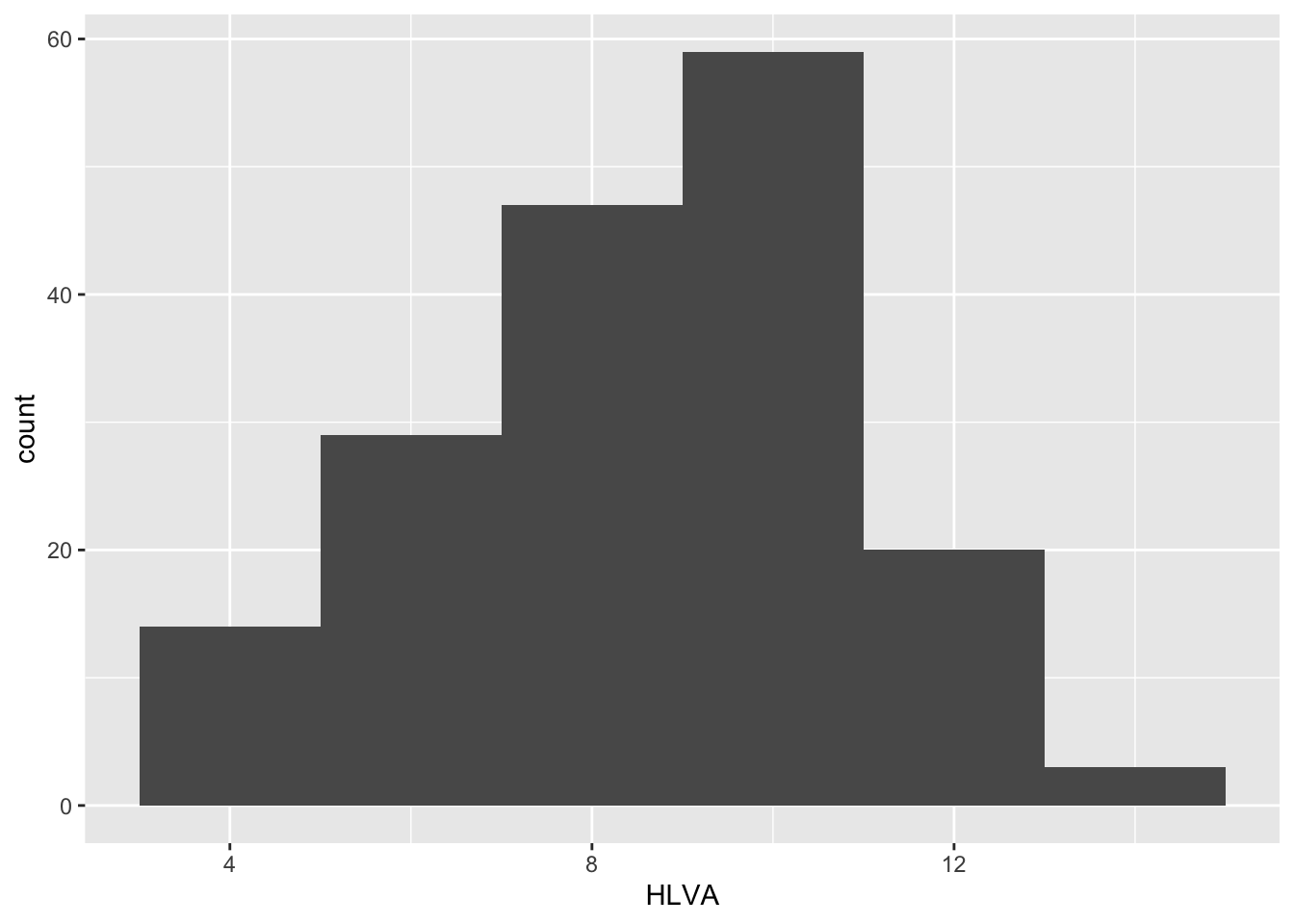

Q.10. Edit the colour of the background using theme_bw()

ggplot(data = study.two.gen, aes(x = HLVA)) + 
  geom_histogram(binwidth = 2) +
  theme_bw()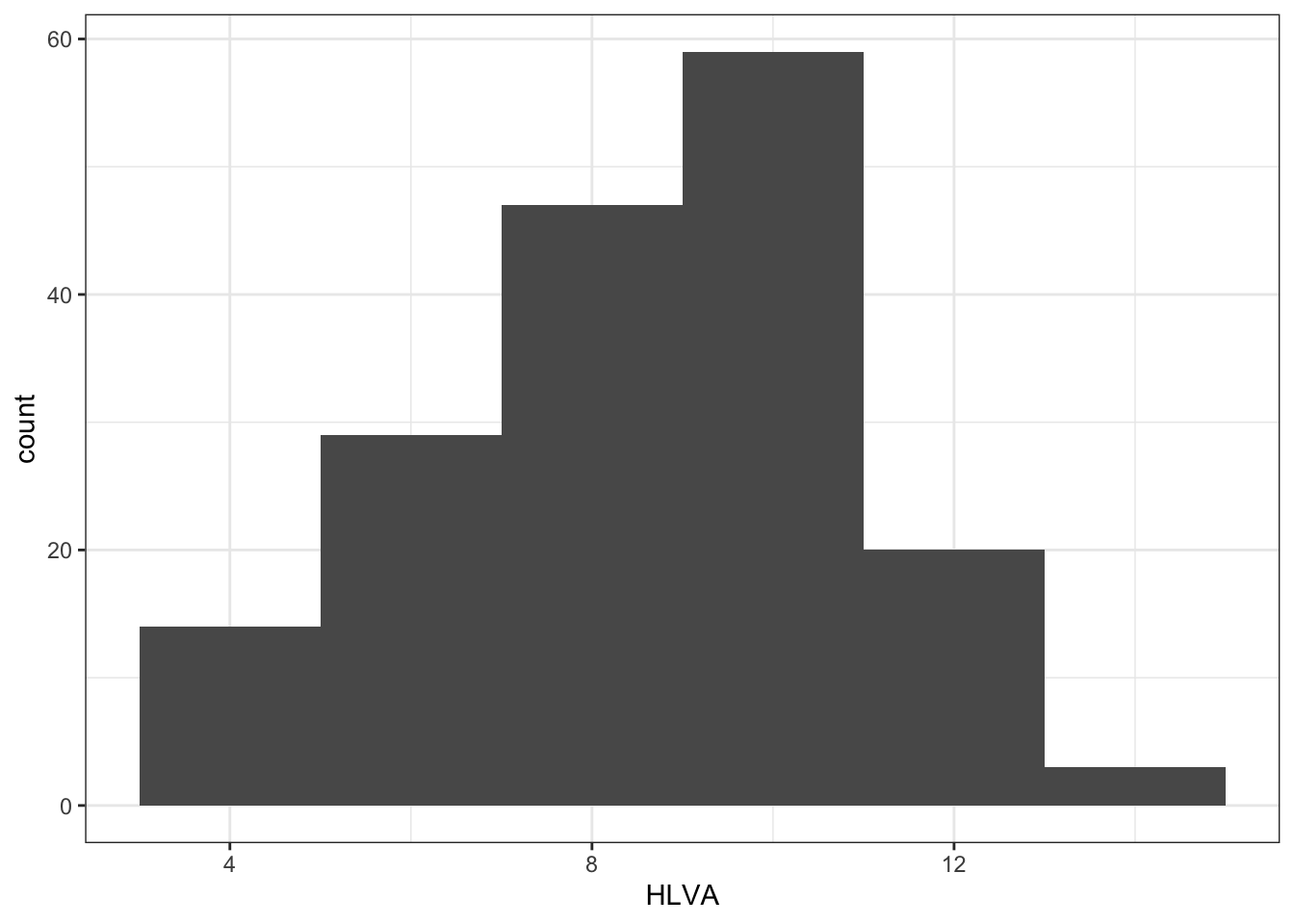

Q.11. Edit the appearance of the labels using labs()

ggplot(data = study.two.gen, aes(x = HLVA)) + 
  geom_histogram(binwidth = 2) +
  theme_bw() +
  labs(x = "HLVA", y = "count")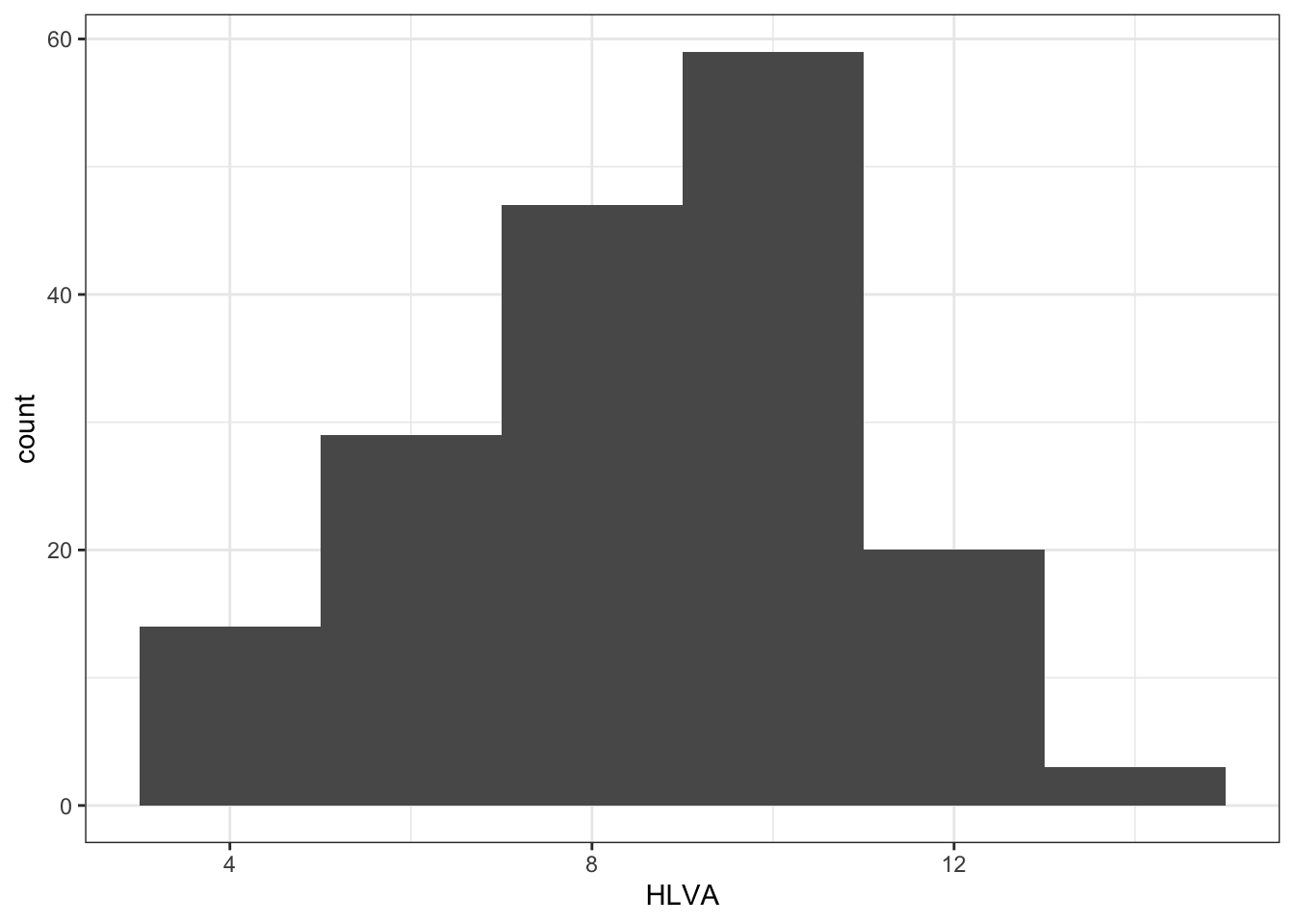

Notice how, if you are doing edits in steps, one line at a time, each line in your code except the last one ends in a +.

What we are doing is telling R we want this + this + this … Each line then adds an extra step.

You can break this code by not adding a + at the end of each bit (except the last line).

Notice that how to break the code, and how to figure out how to fix the break, are discussed in the how-to .R

Step 5: Now draw scatterplots to examine associations between variables

Task 8 – Create a scatterplot to examine the association between some variables

We are working with geom_point() and you need x and y aesthetic mappings

ggplot(data = study.two.gen, aes(x = HLVA, y = mean.acc)) +
  geom_point()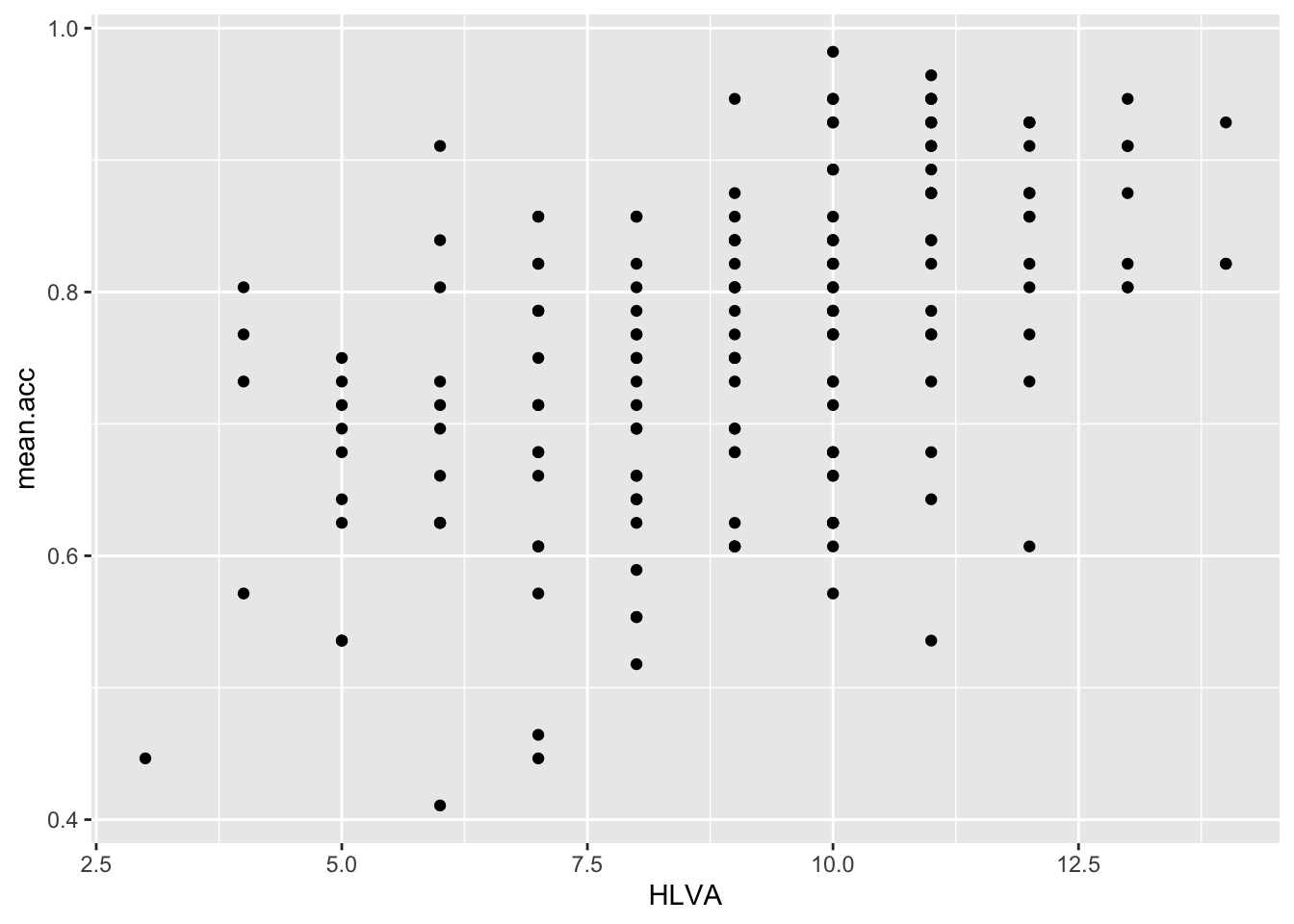

This plot shows the possible association between x-axis variable HLVA and y-axis variable mean.acc.

The plot code moves through the following steps:

ggplot(...) make a plot
ggplot(data = study.two.gen, ...) with the study.two.gen dataset
ggplot(...aes(x = HLVA, y = mean.acc)) using two aesthetic mappings:

x = HLVAmapHLVA` values to x-axis (horizontal, left to right) positions
y = mean.accmapmeann.acc` values to y-axis (vertical, bottom to top) positions

geom_point() show the mappings as points

Task 9 – Now do scatterplots with every numeric predictor variable in the `study.two.gen` dataset

You always want to use as the y-axis variable the outcome mean.acc so:

y = mean.acc

Then you can use each numeric predictor variable as the x-axis variable so:

x = mean.self

Remember what we saw with summary(): not every variable consists of numbers

If the summary() does not show you a mean for a variable, then R does not think that variable is numeric

It can be hard to decide what an association looks like:

Draw the plot, answer the question

ggplot(data = study.two.gen, aes(x = mean.self, y = mean.acc)) +
  geom_point()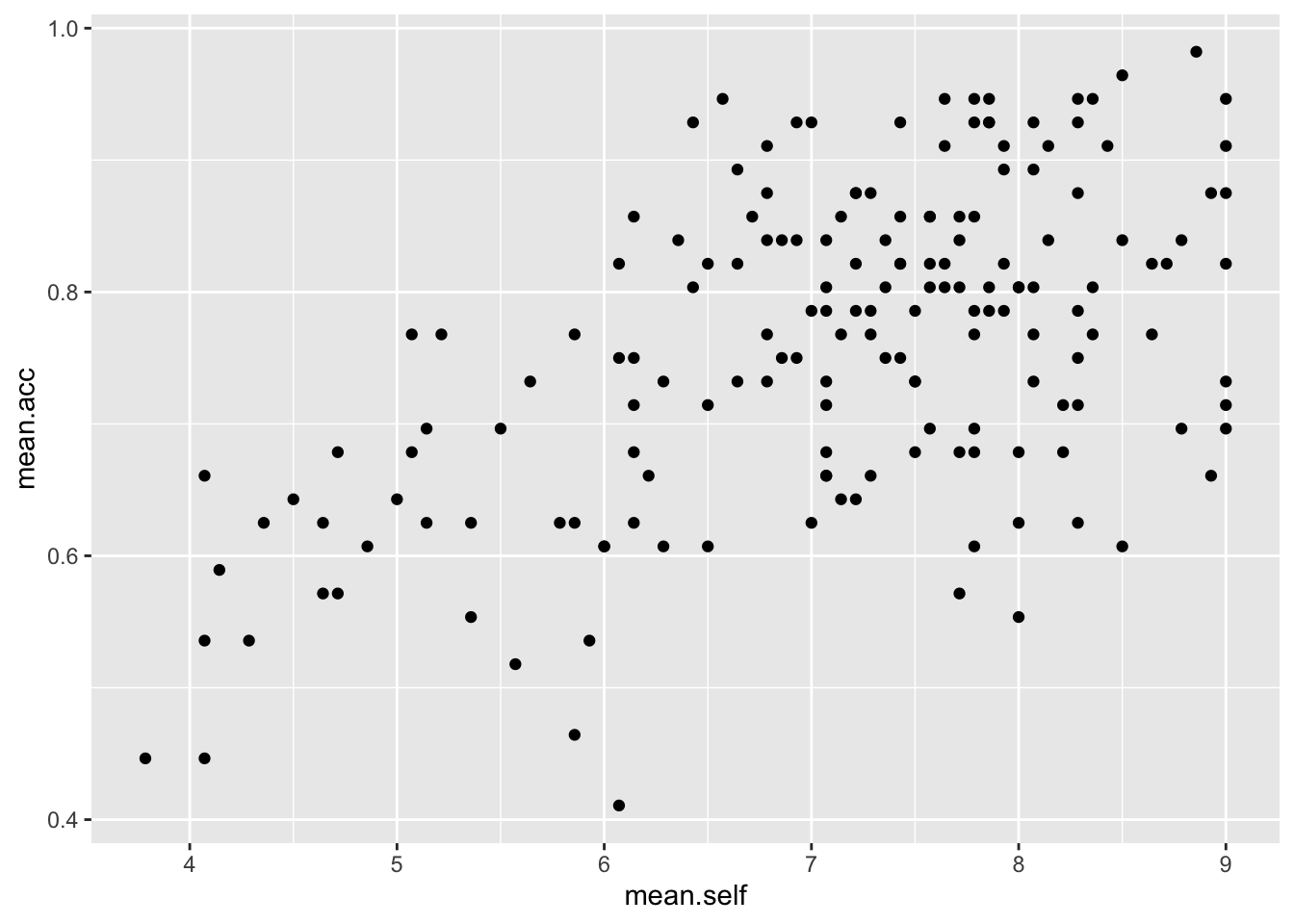

Q.12. What is the shape (direction) of the association between mean.self and mean.acc?
A.12. Increase in mean.self is associated with increase in mean.acc

Draw the plot, answer the question

ggplot(data = study.two.gen, aes(x = AGE, y = mean.acc)) +
  geom_point()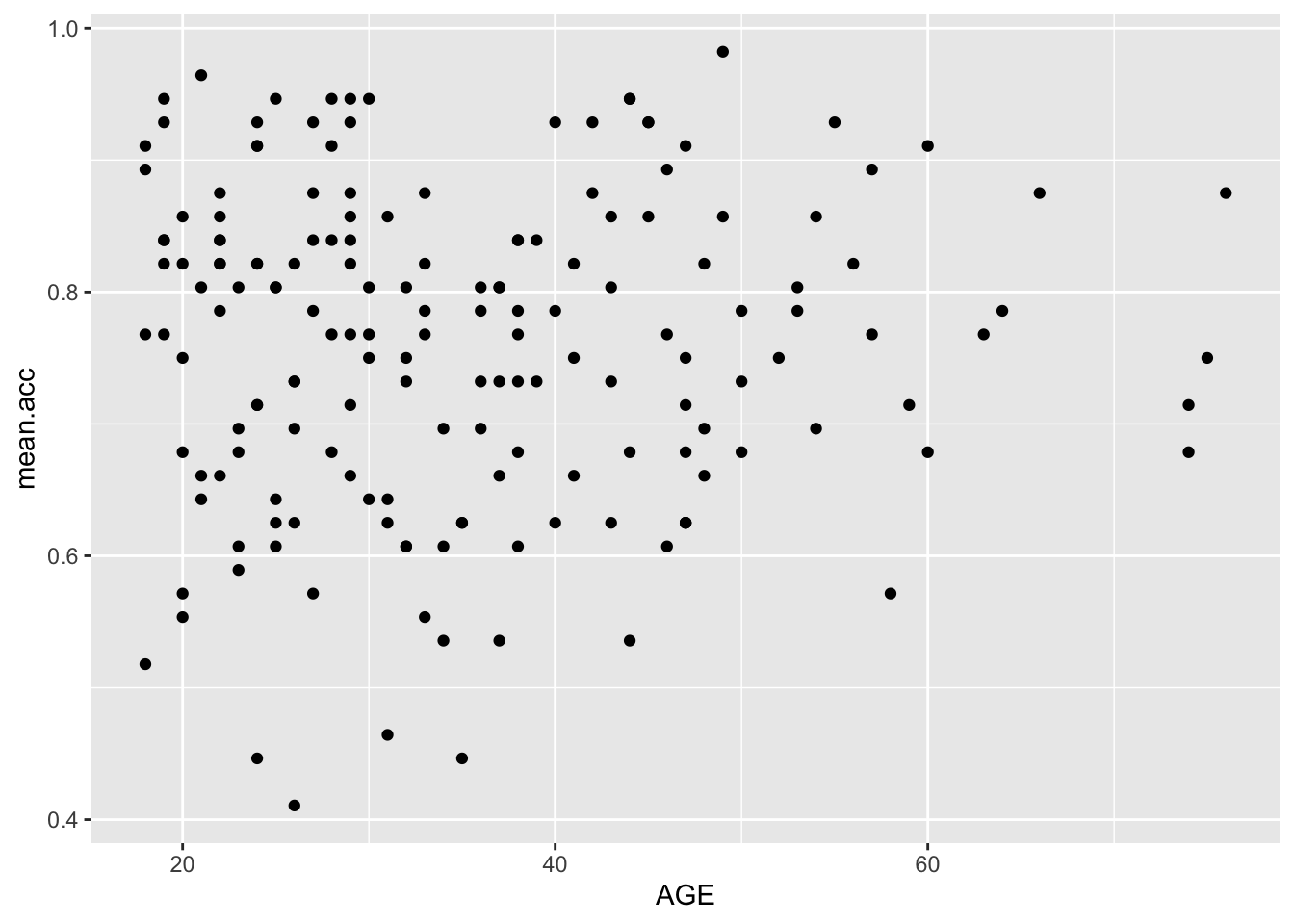

Q.13. What is the shape (direction) of the association between AGE and mean.acc?
A.13. There is no clear association between AGE and mean.acc

Draw the plot, answer the question

ggplot(data = study.two.gen, aes(x = SHIPLEY, y = mean.acc)) +
  geom_point()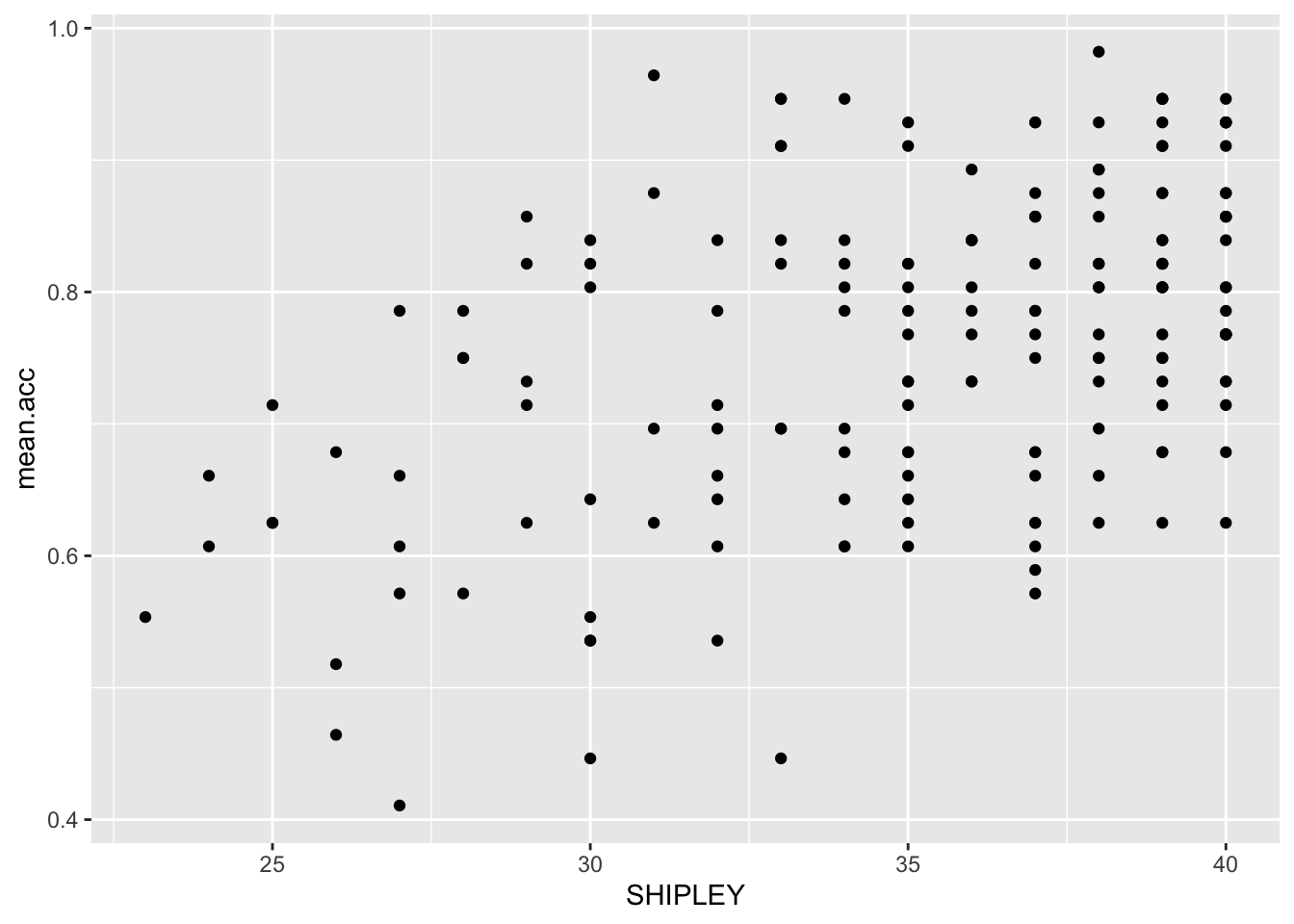

Q.14. What is the shape (direction) of the association between SHIPLEY and mean.acc?
A.14. Increase in SHIPLEY is associated with increase in mean.acc

Draw the plot, answer the question

ggplot(data = study.two.gen, aes(x = HLVA, y = mean.acc)) +
  geom_point()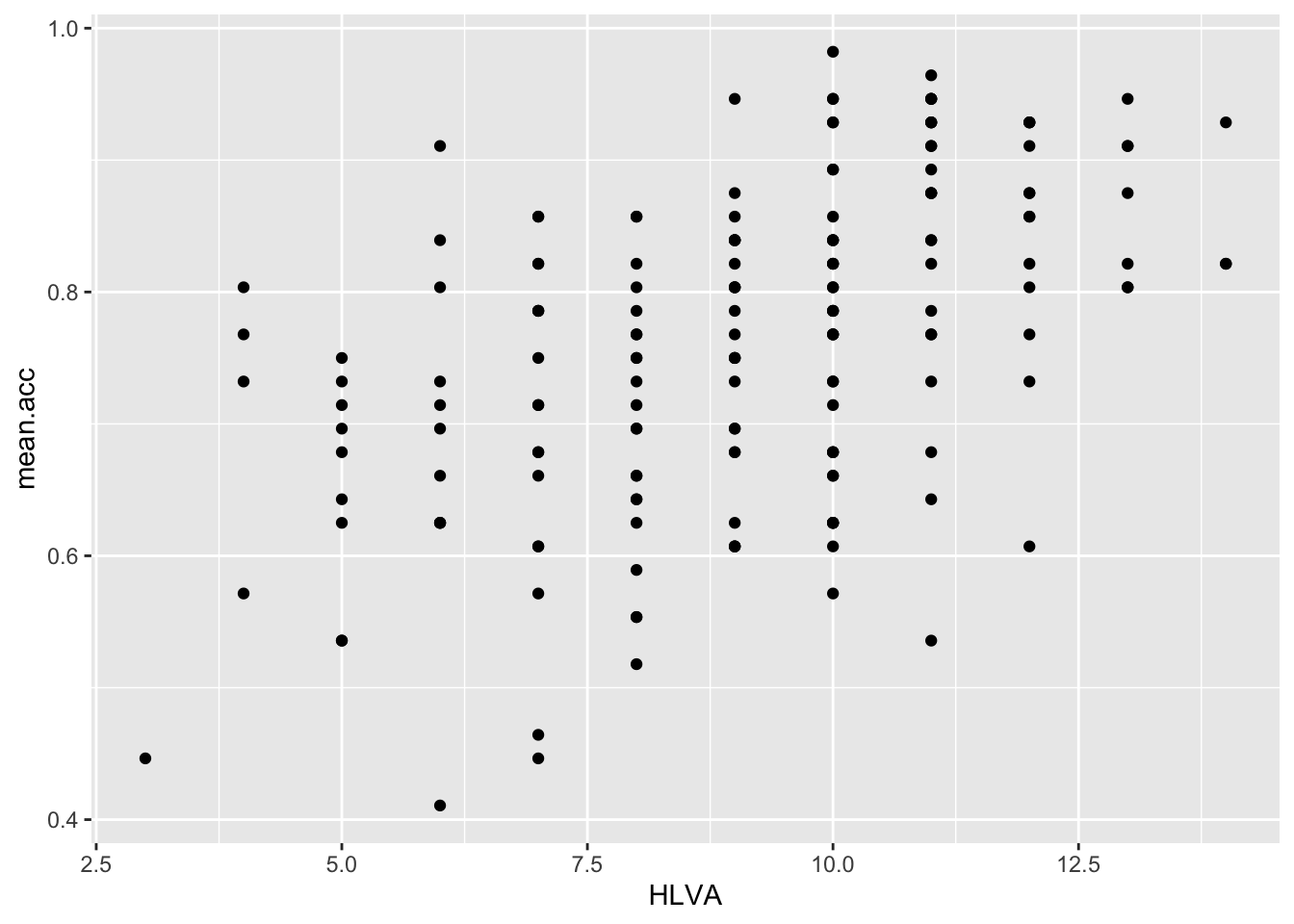

Q.15. – What is the shape (direction) of the association between HLVA and mean.acc?
A.15. Increase in HLVA is associated with increase in mean.acc

Draw the plot, answer the question

ggplot(data = study.two.gen, aes(x = FACTOR3, y = mean.acc)) +
  geom_point()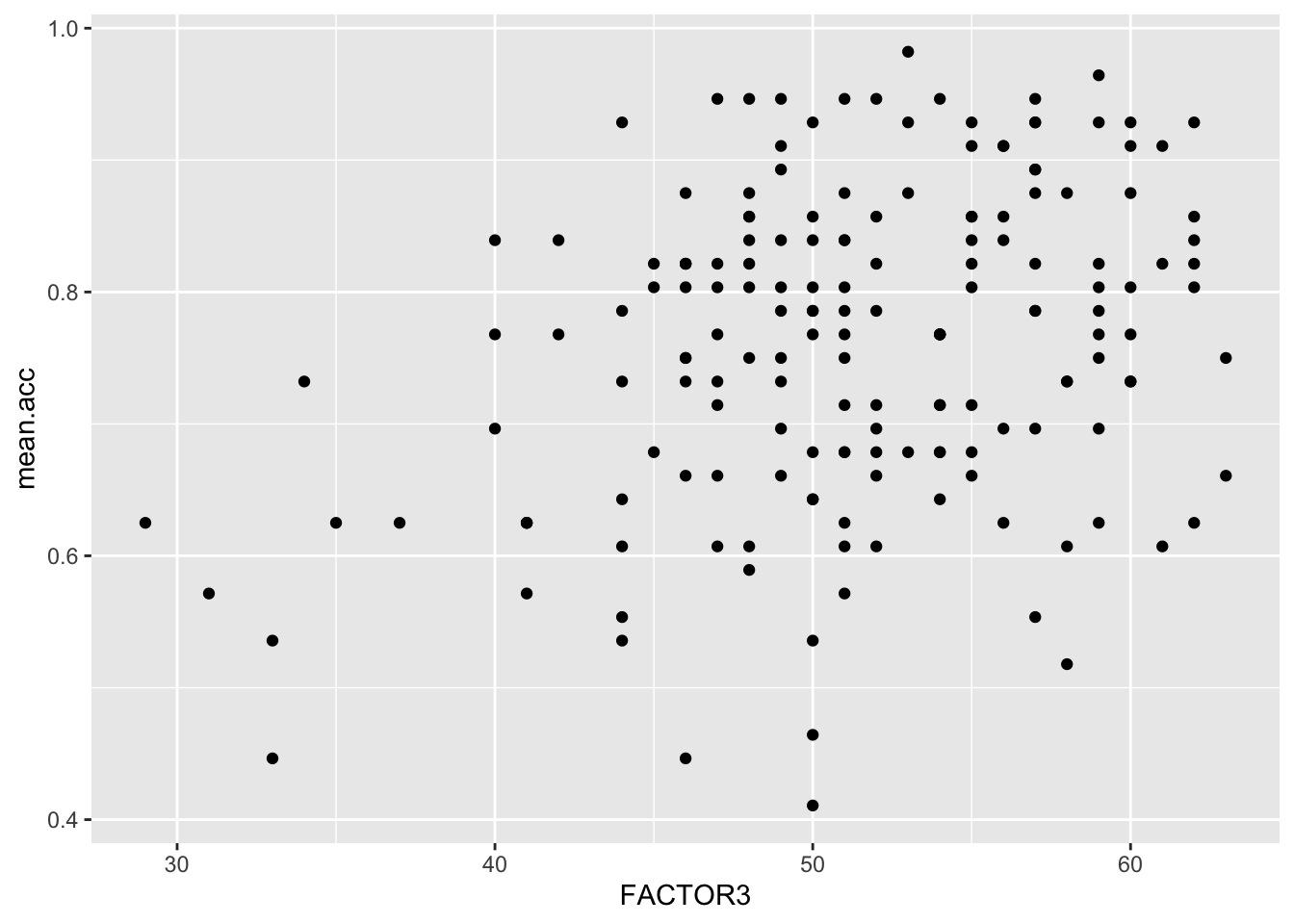

Q.16. What is the shape (direction) of the association between FACTOR3 and mean.acc?
A.16. Increase in FACTOR3 is associated with increase in mean.acc

Draw the plot, answer the question

ggplot(data = study.two.gen, aes(x = QRITOTAL, y = mean.acc)) +
  geom_point()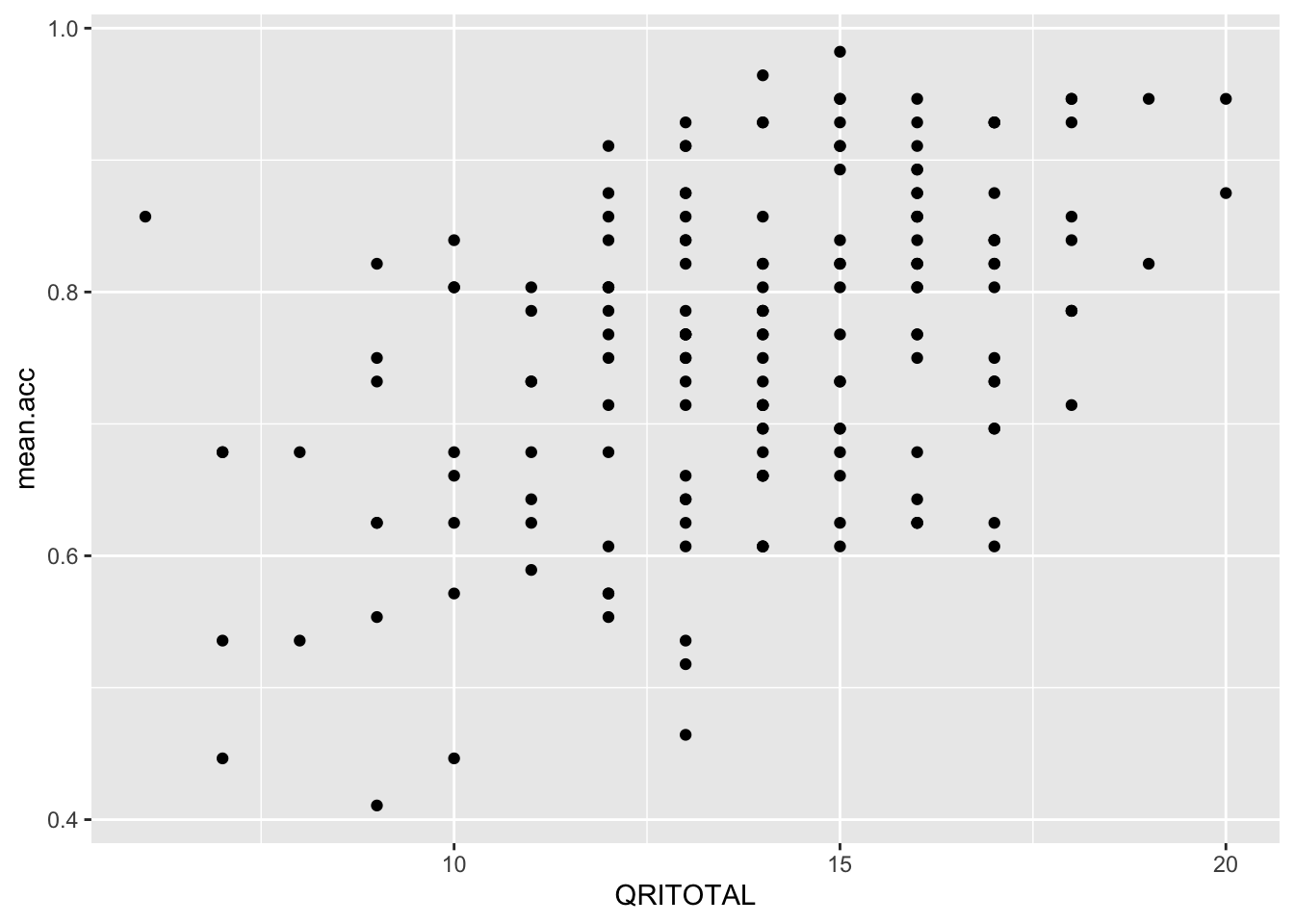

Q.17. What is the shape (direction) of the association between QRITOTAL and mean.acc?
A.17. Increase in QRITOTAL is associated with increase in mean.acc

Step 6: Edit the scatterplots to make them look good

Task 10 – Edit the appearance of one plot step-by-step

Hint: Task 10 – We are going to edit:

the appearance of the points using alpha, size and colour;
the colour of the background using theme_bw();
the appearance of the labels using labs().

Just like with geom_histogram() there is ggplot reference information for the geom you can use here – take a look:

https://ggplot2.tidyverse.org/reference/geom_point.html

You can find some example code and come back here if you are unsure what to do

Questions: Task 10

Q.18. Change the appearance of the points using alpha, size and colour:

ggplot(data = study.two.gen, aes(x = HLVA, y = mean.acc)) +
  geom_point(alpha = 0.5, size = 2, colour = "red")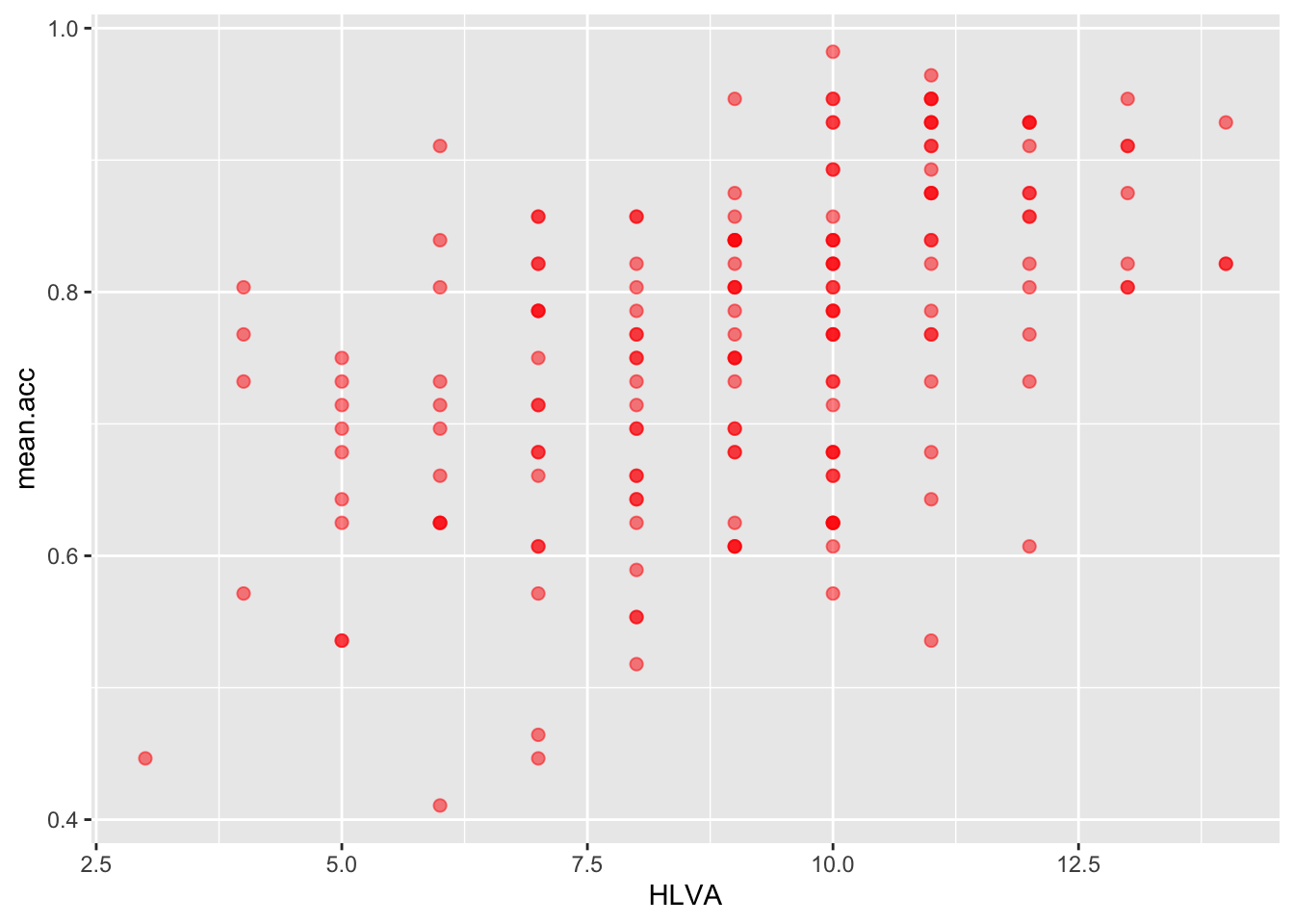

Q.19. Edit the colour of the background using theme_bw()

ggplot(data = study.two.gen, aes(x = HLVA, y = mean.acc)) +
  geom_point(alpha = 0.5, size = 2, colour = "red")   +
  theme_bw()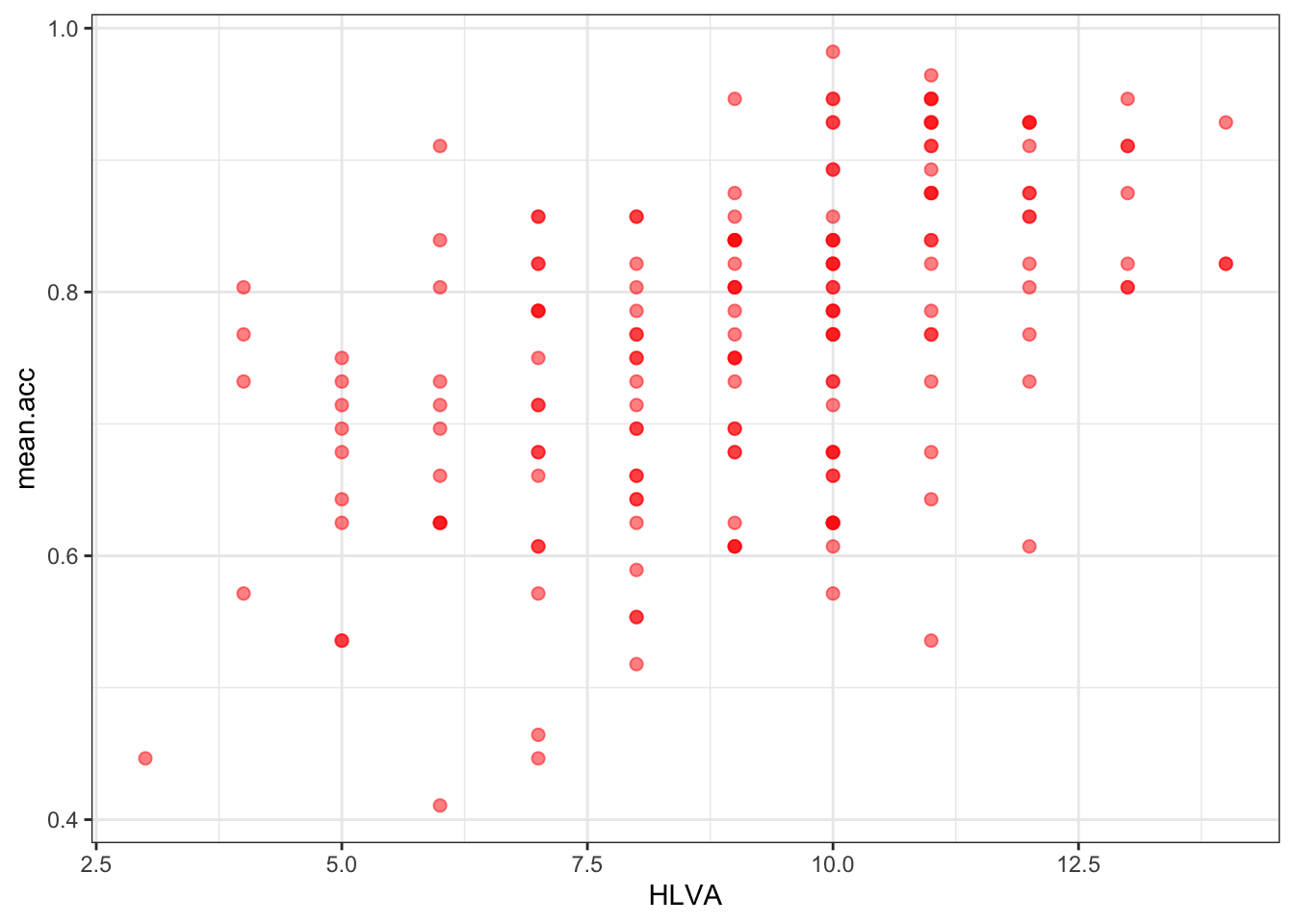

Q.20. Edit the appearance of the labels using labs()

ggplot(data = study.two.gen, aes(x = HLVA, y = mean.acc)) +
  geom_point(alpha = 0.5, size = 2, colour = "red")   +
  theme_bw() +
  labs(x = "HLVA", y = "mean accuracy")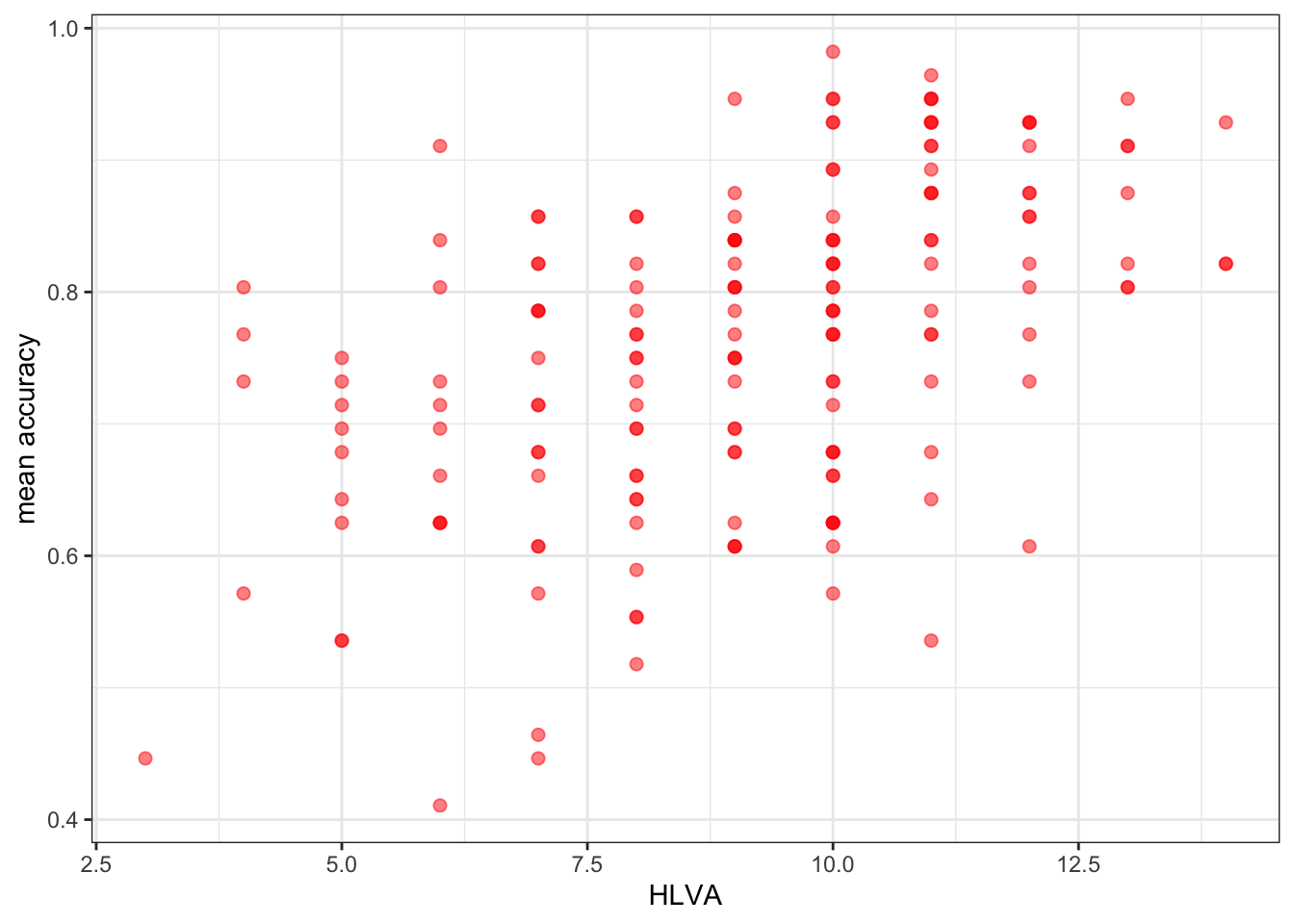

Q.21. Can you find the ggplot reference page?

Do a search with the keywords “ggplot reference geom_point”

A.21. – It is here:

https://ggplot2.tidyverse.org/reference/geom_point.html

Now you: experiment!

Step 7: Use correlation to to answer the research questions

Task 11 – Examine the correlation between mean accuracy (mean.acc) and some numeric predictor variables

We use cor.test()

Q.22. What is r (given as cor in the output) for the correlation between HLVA and mean.acc?

cor.test(study.two.gen$HLVA, study.two.gen$mean.acc, method = "pearson",  alternative = "two.sided")


    Pearson's product-moment correlation

data:  study.two.gen$HLVA and study.two.gen$mean.acc
t = 7.5288, df = 170, p-value = 2.866e-12
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.3787626 0.6044611
sample estimates:
      cor 
0.5000559

A.22. r = 0.5000559
Q.23. Is the correlation significant?
A.23. r is significant
Q.24. What are the values for t and p for the significance test for the correlation?
A.24. t = 7.5288, p = 2.866e-12
Q.25. What do you conclude, given the correlation results? (Maybe draw a scatterplot to examine the shape of the association.)
A.25. HLVA and mean.acc are positively correlated suggesting that as HLVA scores increase so also do mean.acc scores
Q.26. What is r (given as cor in the output) for the correlation between mean.self and mean.acc?

cor.test(study.two.gen$mean.self, study.two.gen$mean.acc, method = "pearson",  alternative = "two.sided")


    Pearson's product-moment correlation

data:  study.two.gen$mean.self and study.two.gen$mean.acc
t = 8.4991, df = 170, p-value = 9.356e-15
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.4317217 0.6431596
sample estimates:
      cor 
0.5460792

A.26. r = 0.5460792
Q.27. Is the correlation between AGE and mean.acc significant?

cor.test(study.two.gen$AGE, study.two.gen$mean.acc, method = "pearson",  alternative = "two.sided")


    Pearson's product-moment correlation

data:  study.two.gen$AGE and study.two.gen$mean.acc
t = 0.30121, df = 170, p-value = 0.7636
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.1269774  0.1721354
sample estimates:
       cor 
0.02309589

A.27. r is not significant
Q.28. What are the values for t and p for the significance test for the correlation between QRITOTAL and mean.acc?

cor.test(study.two.gen$QRITOTAL, study.two.gen$mean.acc, method = "pearson",  alternative = "two.sided")


    Pearson's product-moment correlation

data:  study.two.gen$QRITOTAL and study.two.gen$mean.acc
t = 6.4711, df = 170, p-value = 9.993e-10
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.3159538 0.5571417
sample estimates:
    cor 
0.44457

A.28. t = 6.4711, p = 9.993e-10
Q.29. What do you conclude, given the correlation results, about the association between SHIPLEY and mean.acc?

cor.test(study.two.gen$SHIPLEY, study.two.gen$mean.acc, method = "pearson",  alternative = "two.sided")


    Pearson's product-moment correlation

data:  study.two.gen$SHIPLEY and study.two.gen$mean.acc
t = 6.8493, df = 170, p-value = 1.299e-10
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.3390103 0.5746961
sample estimates:
      cor 
0.4650537

A.29. SHIPLEY and mean.acc are positively correlated suggesting that as HLVA scores increase so also do mean.acc scores

Introduction

Naming things

The data we will be using

Answers

Step 1: Set-up

Task 1 – Run code to empty the R environment

Task 2 – Run code to load relevant libraries

Step 2: Load the data

Task Task 3 – Read in the data file we will be using

Task 4 – Inspect the data file

Task 5 – Change the class or type of the variable ETHNICITY to factor

Step 3: Use histograms to examine the distributions of variables

Task 6 – Draw histograms to examine the distributions of variables

Hint: Task 6

Questions: Task 6

Step 4: Edit your plots to make them look good

Task 7 – Edit the appearance of a histogram plot for one numeric variable

Step 5: Now draw scatterplots to examine associations between variables

Task 8 – Create a scatterplot to examine the association between some variables

Task 9 – Now do scatterplots with every numeric predictor variable in the study.two.gen dataset

Draw the plot, answer the question

Draw the plot, answer the question

Draw the plot, answer the question

Draw the plot, answer the question

Draw the plot, answer the question

Draw the plot, answer the question

Step 6: Edit the scatterplots to make them look good

Task 10 – Edit the appearance of one plot step-by-step

Hint: Task 10 – We are going to edit:

Questions: Task 10

Now you: experiment!

Step 7: Use correlation to to answer the research questions

Task 11 – Examine the correlation between mean accuracy (mean.acc) and some numeric predictor variables

Task 5 – Change the class or type of the variable `ETHNICITY` to factor

Task 9 – Now do scatterplots with every numeric predictor variable in the `study.two.gen` dataset