2023-24-PSYC122-w18-workbook-answers

Author

Rob Davies

Published

March 4, 2024

Introduction

In Week 18, we aim to further develop skills in working with the linear model.

We do this to learn how to answer research questions like:

What person attributes predict success in understanding?
Can people accurately evaluate whether they correctly understand written health information?

These kinds of research questions can be answered using methods like the linear model.

When we do these analyses, we need to think about how we report the results:

we usually need to report information about the kind of model we specify;
and we will need to report the nature of the association estimated in our model.

We usually need to decide:

is the association significant?
does the association reflect a positive or negative relationship between outcome and predictor?
and is the association we see in our sample data relatively strong or weak?

We will consolidate and extend learning on data visualization:

focusing on how we edit ggplot() code to produce professional looking plots.

Naming things

I will format dataset names like this:

study-two-general-participants.csv

I will also format variable (data column) names like this: variable

I will also format value or other data object (e.g. cell value) names like this: studyone

I will format functions and library names like this: e.g. function ggplot() or e.g. library {tidyverse}.

The data we will be using

In this activity, we use data from a second 2020 study of the response of adults from a UK national sample to written health information:

study-two-general-participants.csv

Answers

Step 1: Set-up

To begin, we set up our environment in R.

Task 1 – Run code to empty the R environment

rm(list=ls())

Task 2 – Run code to load relevant libraries

library("ggeffects")
library("tidyverse")

Warning: package 'tidyr' was built under R version 4.1.1

Warning: package 'purrr' was built under R version 4.1.1

Warning: package 'stringr' was built under R version 4.1.1

── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr     1.1.4     ✔ readr     2.1.4
✔ forcats   1.0.0     ✔ stringr   1.5.0
✔ ggplot2   3.4.4     ✔ tibble    3.2.1
✔ lubridate 1.9.2     ✔ tidyr     1.3.0
✔ purrr     1.0.1     
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

Step 2: Load the data

Task 3 – Read in the data file we will be using

The data file is called:

study-two-general-participants.csv

Use the read_csv() function to read the data file into R:

study.two.gen <- read_csv("study-two-general-participants.csv")

Rows: 172 Columns: 12
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (5): participant_ID, study, GENDER, EDUCATION, ETHNICITY
dbl (7): mean.acc, mean.self, AGE, SHIPLEY, HLVA, FACTOR3, QRITOTAL

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

When you read the data file in, give the data object you create a distinct name e.g. study.two.gen.

Task 4 – Inspect the data file

Use the summary() or head() functions to take a look.

head(study.two.gen)

# A tibble: 6 × 12
  participant_ID mean.acc mean.self study     AGE SHIPLEY  HLVA FACTOR3 QRITOTAL
  <chr>             <dbl>     <dbl> <chr>   <dbl>   <dbl> <dbl>   <dbl>    <dbl>
1 studytwo.1        0.411      6.07 studyt…    26      27     6      50        9
2 studytwo.10       0.607      8.5  studyt…    38      24     9      58       15
3 studytwo.100      0.875      8.93 studyt…    66      40    13      60       20
4 studytwo.101      0.964      8.5  studyt…    21      31    11      59       14
5 studytwo.102      0.714      7.07 studyt…    74      35     7      52       18
6 studytwo.103      0.768      5.07 studyt…    18      40    11      54       15
# ℹ 3 more variables: GENDER <chr>, EDUCATION <chr>, ETHNICITY <chr>

summary(study.two.gen)

 participant_ID        mean.acc        mean.self        study          
 Length:172         Min.   :0.4107   Min.   :3.786   Length:172        
 Class :character   1st Qu.:0.6786   1st Qu.:6.411   Class :character  
 Mode  :character   Median :0.7679   Median :7.321   Mode  :character  
                    Mean   :0.7596   Mean   :7.101                     
                    3rd Qu.:0.8393   3rd Qu.:7.946                     
                    Max.   :0.9821   Max.   :9.000                     
      AGE           SHIPLEY           HLVA           FACTOR3     
 Min.   :18.00   Min.   :23.00   Min.   : 3.000   Min.   :29.00  
 1st Qu.:25.00   1st Qu.:32.75   1st Qu.: 7.750   1st Qu.:47.00  
 Median :32.50   Median :36.00   Median : 9.000   Median :51.00  
 Mean   :35.37   Mean   :35.13   Mean   : 9.064   Mean   :51.24  
 3rd Qu.:44.00   3rd Qu.:39.00   3rd Qu.:11.000   3rd Qu.:56.25  
 Max.   :76.00   Max.   :40.00   Max.   :14.000   Max.   :63.00  
    QRITOTAL        GENDER           EDUCATION          ETHNICITY        
 Min.   : 6.00   Length:172         Length:172         Length:172        
 1st Qu.:12.00   Class :character   Class :character   Class :character  
 Median :14.00   Mode  :character   Mode  :character   Mode  :character  
 Mean   :13.88                                                           
 3rd Qu.:16.00                                                           
 Max.   :20.00

Even though you have done this before, you will want to do it again, here, and pay particular attention to:

summary information about the numeric variables;
summary information about variables of class: character.

Step 3: Use a linear model to to answer the research questions – one predictor

Revise: practice to strengthen skills

Revise: We start by revising how to use lm() with one predictor

One of our research questions is:

Can people accurately evaluate whether they correctly understand written health information?

We can address this question by examining whether someone’s rated evaluation of their own understanding matches their performance on a test of that understanding, and by investigating what variables predict variation in mean self-rated accuracy.

Note that ratings of accuracy are ordinal data but that, here, we may choose to examine the average of participants’ ratings of their own understanding of health information to keep our analysis fairly simple.
For these data, participants were asked to respond to questions about health information to get mean.acc scores and then were asked to rate their own understanding of the same information.

If you can evaluate your own understanding then ratings of understanding should be associated with performance on tests of understanding

Task 5 – Estimate the relation between outcome mean self-rated accuracy (`mean.self`) and tested accuracy of understanding (`mean.acc`)

hint: Task 5

For these data, participants were asked to respond to questions about health information to get mean.acc scores and were asked to rate their own understanding of the same information.

hint: Task 5

We can use lm() to estimate whether the ratings of accuracy actually predict the outcome tested accuracy levels.

model <- lm(mean.self ~ mean.acc, data = study.two.gen)
summary(model)


Call:
lm(formula = mean.self ~ mean.acc, data = study.two.gen)

Residuals:
     Min       1Q   Median       3Q      Max 
-2.47926 -0.62782  0.02038  0.65403  2.37788 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   2.8725     0.5037   5.703 5.12e-08 ***
mean.acc      5.5670     0.6550   8.499 9.36e-15 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.032 on 170 degrees of freedom
Multiple R-squared:  0.2982,    Adjusted R-squared:  0.2941 
F-statistic: 72.24 on 1 and 170 DF,  p-value: 9.356e-15

In R analysis code, we write method(outcome ~ predictor) so:

lm(mean.self ~ mean.acc, data = study.two.gen)

gets us an analysis of whether or how mean.self predicts variation in outcome mean.acc.

If you look at the model summary you can answer the following questions.

Questions: Task 5

Q.1. What is the estimate for the coefficient of the effect of the predictor mean.acc on the outcome mean.self in this model?
A.1. 5.5670
Q.2. Is the effect significant?
A.2. It is significant, p < .05
Q.3. What are the values for t and p for the significance test for the coefficient?
A.3. t = 8.499, p = 9.36e-15
Q.4. What do you conclude is the answer to the research question, given the linear model results?
A.4. The model slope estimate suggests that higher levels of tested understanding can predict higher levels of rated understanding so, yes: it does appear that people can evaluate their own understanding.
Q.5. What is the F-statistic for the regression? Report F, DF and the p-value.
A.5. F-statistic: 72.24 on 1 and 170 DF, p-value: 9.356e-15
Q.6. Is the regression significant?
A.6. Yes: the regression is significant.
Q.7. What is the Adjusted R-squared?
A.7. Adjusted R-squared: 0.2941
Q.8. Explain in words what this R-squared value indicates?
A.8. The R-squared suggests that about 30% of outcome variance can be explained by the model

Step 4: Use a linear model to to answer the research questions – multiple predictors

Introduce: make some new moves

One of our research questions is:

Can people accurately evaluate whether they correctly understand written health information?

We have already looked at this question by asking whether ratings of understanding predict performance on tests of understanding.

But there is a problem with that analysis – it leaves open the question:

What actually predicts ratings of understanding?

We can look at this follow-up question, next.

Task 6 – Examine the relation between outcome mean self-rated accuracy (`mean.self`) and multiple predictors

Here, the predictors will include:

health literacy (HLVA);
vocabulary (SHIPLEY);
age in years (AGE);
reading strategy (FACTOR3);
as well as average accuracy of the tested understanding of health information (mean.acc).

hint: Task 6 – We use `lm()`, as before, but now specify each variable listed here by variable name

model <- lm(mean.self ~ HLVA + SHIPLEY + FACTOR3 + AGE + mean.acc, 
            data = study.two.gen)
summary(model)


Call:
lm(formula = mean.self ~ HLVA + SHIPLEY + FACTOR3 + AGE + mean.acc, 
    data = study.two.gen)

Residuals:
     Min       1Q   Median       3Q      Max 
-2.72027 -0.49118 -0.00177  0.55561  2.00134 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.561110   0.700632   0.801   0.4244    
HLVA         0.041272   0.034833   1.185   0.2378    
SHIPLEY     -0.046125   0.018701  -2.466   0.0147 *  
FACTOR3      0.063689   0.010747   5.926 1.74e-08 ***
AGE          0.025570   0.005472   4.673 6.12e-06 ***
mean.acc     4.763278   0.708166   6.726 2.69e-10 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.8805 on 166 degrees of freedom
Multiple R-squared:  0.5014,    Adjusted R-squared:  0.4864 
F-statistic: 33.39 on 5 and 166 DF,  p-value: < 2.2e-16

Questions: Task 6

If you look at the model summary you can answer the following questions.

Q.9. What predictors are significant in this model?
A.9. Vocabulary (SHIPLEY), reading strategy (FACTOR3), AGE, and performance on tests of accuracy of understanding (mean.acc) all appear to significantly predict variation in mean ratings of understanding (mean.self).
Q.10. What is the estimate for the coefficient of the effect of the predictor mean.acc in this model?
A.10. 4.763278
Q.11. Is the effect significant?
A.11. It is significant, p < .05
Q.12. What are the values for t and p for the significance test for the coefficient?
A.12. t = 6.726, p = 2.69e-10
Q.13. What do you conclude is the answer to the follow-up question, what actually predicts ratings of understanding?
A.13. Ratings of understanding appear to be predicted by performance on tests of accuracy of understanding, together with variation in age, vocabulary knowledge, health literacy and reading strategy

Step 5: Understanding linear model predictions by comparing one outcome-predictor relation

Next, we focus in on whether mean.self predicts mean.acc or, in reverse, whether mean.acc predicts mean.self?

Note that a comparison between these models teaches us something important about what it is that linear models predict.
Q.14. Why do you think it appears that the slope coefficient estimate is different if you compare :

The model mean.acc ~ mean.self versus
The model mean.self ~ mean.acc?

hint: Q.14. You want to fit two simple models here, using the verbal description in the Q.14 wording.

1. The model mean.acc ~ mean.self

model.1 <- lm(mean.acc ~ mean.self, data = study.two.gen)
summary(model.1)


Call:
lm(formula = mean.acc ~ mean.self, data = study.two.gen)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.293692 -0.069200  0.005422  0.080041  0.215240 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.379182   0.045415   8.349 2.31e-14 ***
mean.self   0.053566   0.006303   8.499 9.36e-15 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1013 on 170 degrees of freedom
Multiple R-squared:  0.2982,    Adjusted R-squared:  0.2941 
F-statistic: 72.24 on 1 and 170 DF,  p-value: 9.356e-15

2. The model mean.self ~ mean.acc

model.2 <- lm(mean.self ~ mean.acc, 
              data = study.two.gen)
summary(model.2)


Call:
lm(formula = mean.self ~ mean.acc, data = study.two.gen)

Residuals:
     Min       1Q   Median       3Q      Max 
-2.47926 -0.62782  0.02038  0.65403  2.37788 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   2.8725     0.5037   5.703 5.12e-08 ***
mean.acc      5.5670     0.6550   8.499 9.36e-15 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.032 on 170 degrees of freedom
Multiple R-squared:  0.2982,    Adjusted R-squared:  0.2941 
F-statistic: 72.24 on 1 and 170 DF,  p-value: 9.356e-15

hint: Q.14. You may benefit here by reflecting on the lm-intro lecture and practical materials, especially where they concern predictions.
A.14. Linear models are prediction models. We use them to predict variation in outcomes given some set of predictor variables. Predictions will necessarily be scaled in the same way as the outcome variable.

So, to expand on that explanation a bit more, to help understanding – the answer is:

If we have the model, mean.acc ~ mean.self then this means that the outcome is mean.acc.

So if we are predicting change in outcome mean.acc, which is scaled 0-1, then we are looking at coefficients that will lie somewhere on the same scale (also 0-1).
Here: the model estimate suggests that each unit change in values of the variable mean.self predicts an increase of 0.053566 in mean.acc.

Whereas if we have the model, mean.self ~ mean.acc then this means that the outcome is mean.self.

So if we are predicting change in outcome mean.self, which is scaled 1-9 , then we are looking at coefficients that will lie somewhere on the same scale (also 1-9).
Here: the model estimate suggests that unit change in mean.acc predicts increase of 5.5670 in mean.self.

Note that:

Where we reference model estimates, here, we are looking at the values in the Estimate column of the lm() model summary.
These estimates give us the expected or predicted change in the outcome, given change in the predictor variable named on that row.

Remember that:

mean.acc is scaled from 0 to 1 because it represents the average accuracy of the responses made by study participants to questions about health texts. This average has to have a minimum of 0 (no responses correct) and a maximum of 1 (all responses correct). The average is calculated by adding up all the correct answers and dividing by the number of questions answered by each participant.
mean.self is scaled from 1 to 9 bcause it represents the average self-rated accuracy of understanding. Participants are asked to rate on a scale form 1 (not all) to 9 (very well) how well they think they understand a health information text. The average is calculated by adding up all the ratings and dividing by the number of texts responded to by each participant.

The important lesson, here, is that estimates of predictor effects are scaled in terms of predicted change in the outcome, so whatever scale the outcome measurement is in determines how big or small the predictor coefficient estimates can be.

We can visualize this to see what it means in practice.

Q.15. Can you plot the predictions from each model?
A.15. Here is the code to plot the predictions from both models.

First fit the models.

Remember to give each model object distinct names.

model.1 <- lm(mean.acc ~ mean.self, data = study.two.gen)
summary(model.1)


Call:
lm(formula = mean.acc ~ mean.self, data = study.two.gen)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.293692 -0.069200  0.005422  0.080041  0.215240 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.379182   0.045415   8.349 2.31e-14 ***
mean.self   0.053566   0.006303   8.499 9.36e-15 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1013 on 170 degrees of freedom
Multiple R-squared:  0.2982,    Adjusted R-squared:  0.2941 
F-statistic: 72.24 on 1 and 170 DF,  p-value: 9.356e-15

model.2 <- lm(mean.self ~ mean.acc, 
            data = study.two.gen)
summary(model.2)


Call:
lm(formula = mean.self ~ mean.acc, data = study.two.gen)

Residuals:
     Min       1Q   Median       3Q      Max 
-2.47926 -0.62782  0.02038  0.65403  2.37788 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   2.8725     0.5037   5.703 5.12e-08 ***
mean.acc      5.5670     0.6550   8.499 9.36e-15 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.032 on 170 degrees of freedom
Multiple R-squared:  0.2982,    Adjusted R-squared:  0.2941 
F-statistic: 72.24 on 1 and 170 DF,  p-value: 9.356e-15

Second get the predictions:

dat.1 <- ggpredict(model.1, "mean.self")
dat.2 <- ggpredict(model.2, "mean.acc")

Third make the prediction plots:

Predictions from the model mean.acc ~ mean.self

plot(dat.1)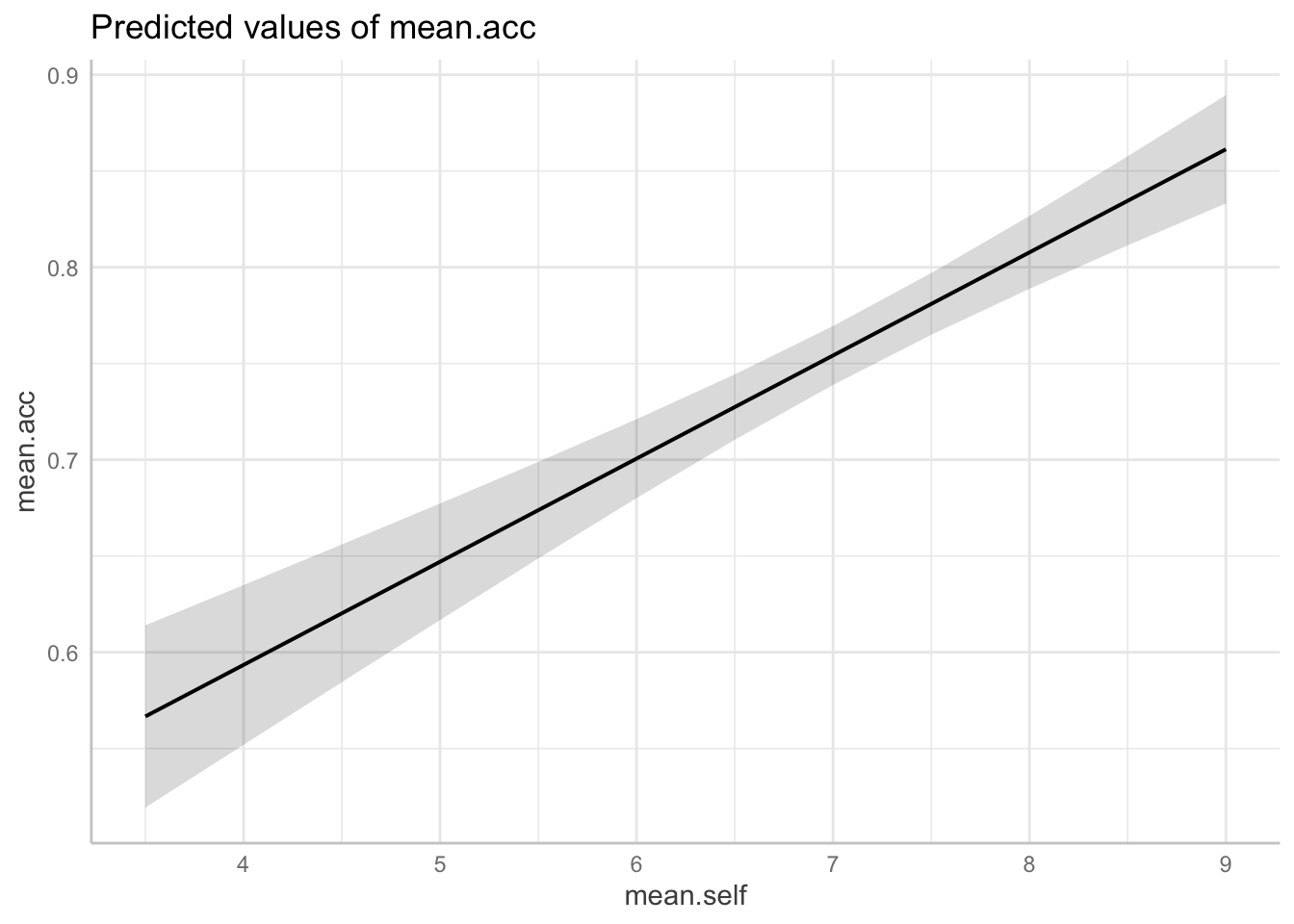

Predictions from the model mean.self ~ mean.acc

plot(dat.2)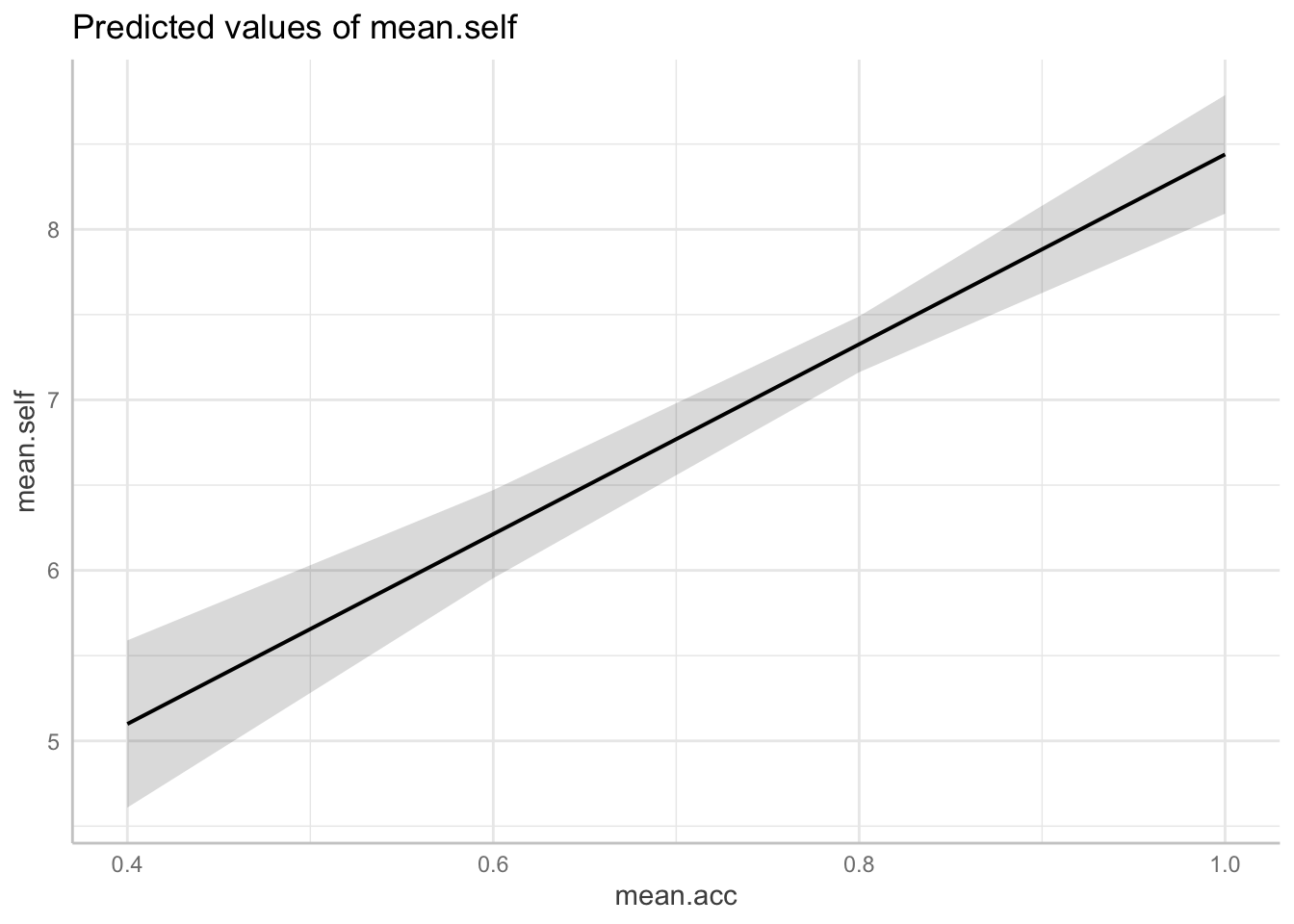

Q.16. Look at the two plots: what do you see?
hint: Q.16. Look at changes in height of the prediction line, given changes in x-axis position of the line
A.16. A side-by-side comparison shows that:

For model mean.acc ~ mean.self increases in mean.self from about 4 to 9 are associated with a change in mean.acc from about .6 to about .85;
For model mean.self ~ mean.acc increases in mean.acc from about 0.4 to 1.0 are associated with a change in mean.self from about 5 to about 9.

Step 6: Estimate the effects of factors as well as numeric variables

Consolidation: build your skills

We have not yet included any categorical or nominal variables as predictors but we can, and should: lm() can cope with any kind of variable as a predictor.

There are different ways to do this, here we ask you to use the R default method.

Task 7 – Fit a linear model to examine what variables predict outcome mean self-rated accuracy of `mean.self`

hint: Task 7 – Include as predictors both numeric variables and categorical variables

Here, our model includes predictors that are both numeric like:

health literacy (HLVA);
vocabulary (SHIPLEY);
AGE;
reading strategy (FACTOR3);
accuracy mean.acc

As well as a categorical or nominal variable like

EDUCATION.

Note: EDUCATION is different because participants are classified by what education category (higher education, further education, secondary school) they report themselves as having received.

model <- lm(mean.self ~ HLVA + SHIPLEY + FACTOR3 + AGE + mean.acc +
                        EDUCATION, 
            data = study.two.gen)
summary(model)


Call:
lm(formula = mean.self ~ HLVA + SHIPLEY + FACTOR3 + AGE + mean.acc + 
    EDUCATION, data = study.two.gen)

Residuals:
     Min       1Q   Median       3Q      Max 
-2.70987 -0.50037  0.01988  0.55965  2.01412 

Coefficients:
                    Estimate Std. Error t value Pr(>|t|)    
(Intercept)         0.487753   0.702049   0.695   0.4882    
HLVA                0.047100   0.034915   1.349   0.1792    
SHIPLEY            -0.044132   0.018719  -2.358   0.0196 *  
FACTOR3             0.061918   0.010771   5.749 4.29e-08 ***
AGE                 0.023997   0.005595   4.289 3.06e-05 ***
mean.acc            4.912833   0.712381   6.896 1.10e-10 ***
EDUCATIONHigher    -0.082217   0.146390  -0.562   0.5751    
EDUCATIONSecondary  0.346161   0.266030   1.301   0.1950    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.8783 on 164 degrees of freedom
Multiple R-squared:  0.5099,    Adjusted R-squared:  0.489 
F-statistic: 24.38 on 7 and 164 DF,  p-value: < 2.2e-16

Q.17. Can you report the overall model and model fit statistics?
A.17.

We fitted a linear model with mean self-rated accuracy as the outcome and with the predictors: health literacy (HLVA), vocabulary (SHIPLEY), reading strategy (FACTOR3), AGE, as well as mean accuracy (mean.acc) and education level (EDUCATION). The model is significant overall, with F(7, 164) = 24.38, p < .001, and explains 49% of variance (adjusted R2 = 0.489).

Q.18. Can you plot the predicted effect of EDUCATION given your model?
hint: Q.18. We first fit the model, including EDUCATION.

model <- lm(mean.self ~ HLVA + SHIPLEY + FACTOR3 + AGE + mean.acc + EDUCATION, 
            data = study.two.gen)

hint: Q.18. We then use the ggpredict() function to get the prediction for the effect of EDUCATION differences on outcome mean.self.

dat <- ggpredict(model, "EDUCATION")
plot(dat)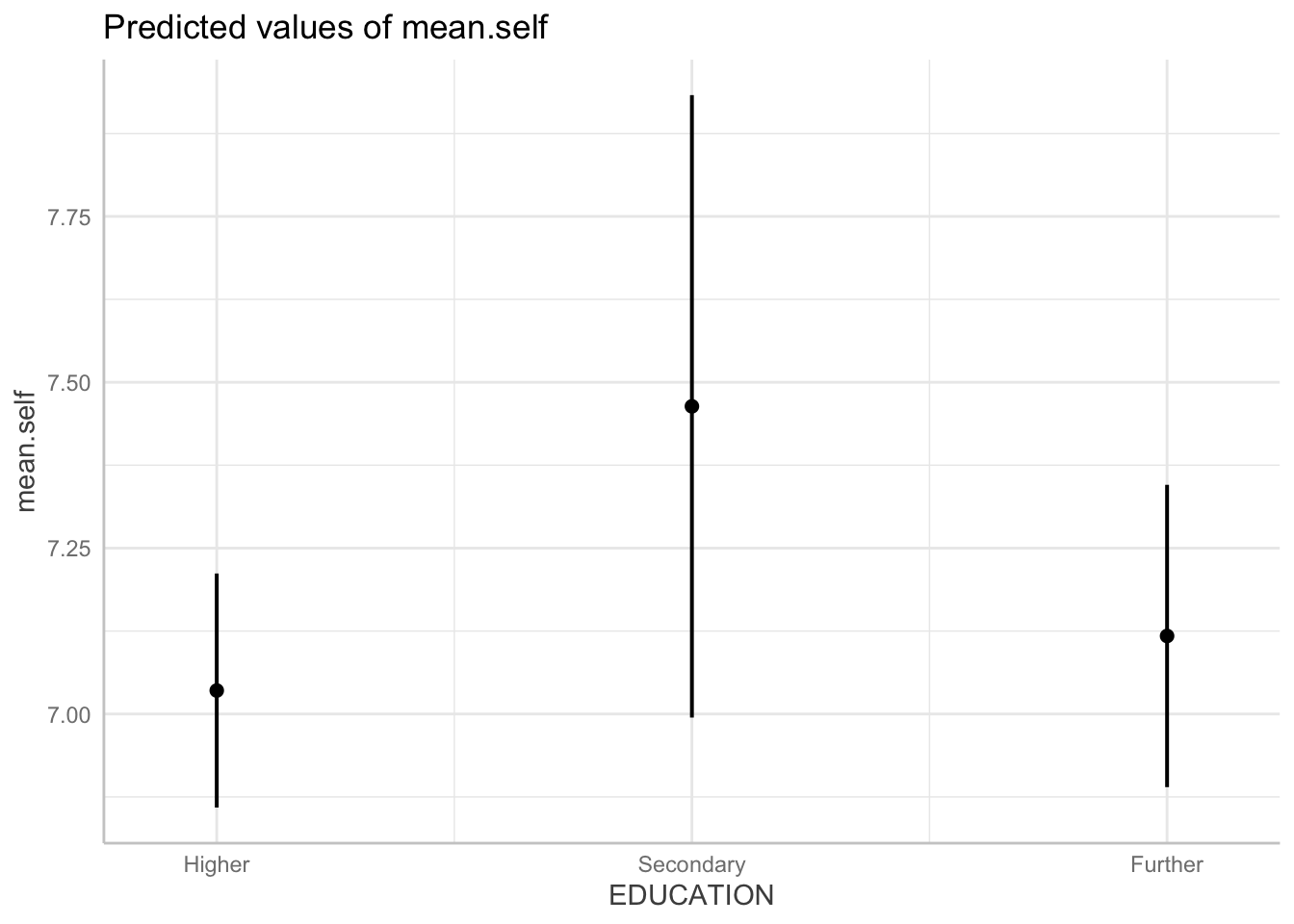

Q.19. The plot should give you dot-and-whisker representations of the estimated mean.self outcome for different levels of EDUCATION. What is the difference in the estimated mean.self between the groups?
hint: Q.19. The effect or prediction plot will show you dot-and-whisker representations of predicted outcome mean.self. In these plots, the dots represent the estimated mean.self while the lines (whiskers) represent confidence intervals.
A.19. The difference in the estimated mean.self between these groups is small: the groups vary between ratings of about 7, 7.10 and 7.5.
Q.20. Compare the difference in the estimated mean.self between these groups, given the plot, with the coefficient estimate from the model summary: what do you see?
A.20. The effect of EDUCATION is presented in the summary as two estimates:
EDUCATIONHigher -0.082217
EDUCATIONSecondary 0.346161

The reference level for EDUCATION is Further.

The estimates therefore show that people with Higher education have mean.self scores about -.08 lower than mean.self for people with Further education.

People with Secondary education have mean.self scores about .35 higher than mean.self for people with Further education.

We are learning some new things here so it is useful to explain them:

Categorical variables or factors and reference levels.

If you have a categorical variable like EDUCATION then when you use it in an analysis, R will look at the different categories (called levels) e.g., here,higher education, further education, secondary school` and it will pick one level to be the reference or baseline level.
The reference is the the level against which other levels are compared.
Here, the reference level is Further (education) simply because, unless you tell R otherwise, it picks the level with a category name that begins earlier in the alphabet as the reference level.

Dot and whisker plots show estimates with confidence intervals.

Dot and whisker plots are a nice way to present a concise visual summary about the estimates we get from prediction models.
Here, the plots show the coefficient estimates from our model (the dots) plus confidence intervals (the lines or “whiskers”).

Confidence intervals are often misunderstood but they are helpful.

Essentially, a confidence interval tells us about we might expect to see using our analysis procedure (Hoekstra et al., 2014).

If we were to repeat the experiment over and over, then 95 % of the time the confidence intervals contain the true mean.

And you can read more about this here

Hoekstra, R., Morey, R. D., Rouder, J. N., & Wagenmakers, E. J. (2014). Robust misinterpretation of confidence intervals. Psychonomic Bulletin & Review, 21, 1157-1164.

Introduction

Naming things

The data we will be using

Answers

Step 1: Set-up

Task 1 – Run code to empty the R environment

Task 2 – Run code to load relevant libraries

Step 2: Load the data

Task 3 – Read in the data file we will be using

Task 4 – Inspect the data file

Step 3: Use a linear model to to answer the research questions – one predictor

Revise: practice to strengthen skills

Revise: We start by revising how to use lm() with one predictor

Task 5 – Estimate the relation between outcome mean self-rated accuracy (mean.self) and tested accuracy of understanding (mean.acc)

hint: Task 5

hint: Task 5

Questions: Task 5

Step 4: Use a linear model to to answer the research questions – multiple predictors

Introduce: make some new moves

Task 6 – Examine the relation between outcome mean self-rated accuracy (mean.self) and multiple predictors

hint: Task 6 – We use lm(), as before, but now specify each variable listed here by variable name

Questions: Task 6

Step 5: Understanding linear model predictions by comparing one outcome-predictor relation

Step 6: Estimate the effects of factors as well as numeric variables

Consolidation: build your skills

Task 7 – Fit a linear model to examine what variables predict outcome mean self-rated accuracy of mean.self

hint: Task 7 – Include as predictors both numeric variables and categorical variables

Task 5 – Estimate the relation between outcome mean self-rated accuracy (`mean.self`) and tested accuracy of understanding (`mean.acc`)

Task 6 – Examine the relation between outcome mean self-rated accuracy (`mean.self`) and multiple predictors

hint: Task 6 – We use `lm()`, as before, but now specify each variable listed here by variable name

Task 7 – Fit a linear model to examine what variables predict outcome mean self-rated accuracy of `mean.self`