This week is a crossover week between Emma and Amy.
Factor Analysis content is needed for learning. Questions will not be asked in the class test in week 20 on the Factor Analysis method.
The rest of this page is split into two parts, Factor Analysis and Binomial Test. They each have their own associated lecture and notes.
Factor Analysis
Factor analysis is an analysis method that aims to take a large number of observed variables, find subsets of the variables that are highly correlated with each other and construct a smaller set of unobserved variables, that we call latent variables.
Factor analysis assumes that when variables are very highly correlated with each other then on one level they could be measuring the same underlying construct. In which case, you can capture only the bits that contribute differentially to the underlying construct and make a new variable from those different parts.
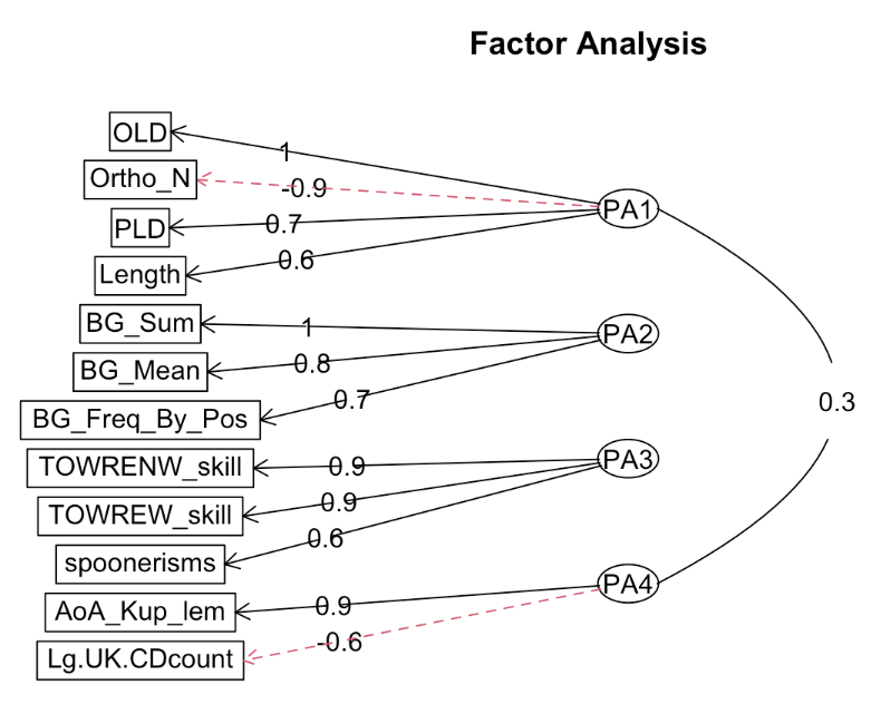
In this diagram, we have a set of observed variables on the left (rectangles). These are the constructs that we measure or observe. They are the columns that we can see in our dataset.
Moving across the page, most of the observed variables are connected by arrows to one of four latent variables (PA1, PA2, PA3, and PA4), on the right. Latent variables are always drawn in ovals or circles on these diagrams. These are the unobserved variables that are made during the factor analysis process.
What goes into the new, latent variables is decided by how well the observed variables correlate with each other. You have already been looking at how well predictor variables correlate with each other during the visualisation part of the analysis workflow (those complicated looking correlation matrices!). When subsets of observed variables correlate well with each other then this could be an indicator that a factor analysis is a feasible method for reducing a large set of variables down to a smaller set.
The values that you see on each of the connecting arrows are how much of the observed variable is contributing to the unobserved variables. We say this is an observed variable’s “loading” onto the latent variable. Higher loading values indicate stronger links to that latent variable.
In 224, you are engaging in questionnaire design, where sets of items are specifically designed to measure one construct. If you have three or more of those items, then you may have the conditions that suggest a factor analysis. In other studies, you may have taken a personality test, or other questionnaire style test where a lot of the questions seemed to ask about similar things. In the big five mini-IPIP scale, the two questions for extraversion are “Am the life of the party” and “Talk to a lot of different people at parties”. The expectation is that if there is indeed an underlying variable behind these two questions, then people’s responses should be similar to both questions.
Factor Analysis Needs Predictor Variables That Are Co-linear
Correlation looks at pairs of numerical variables
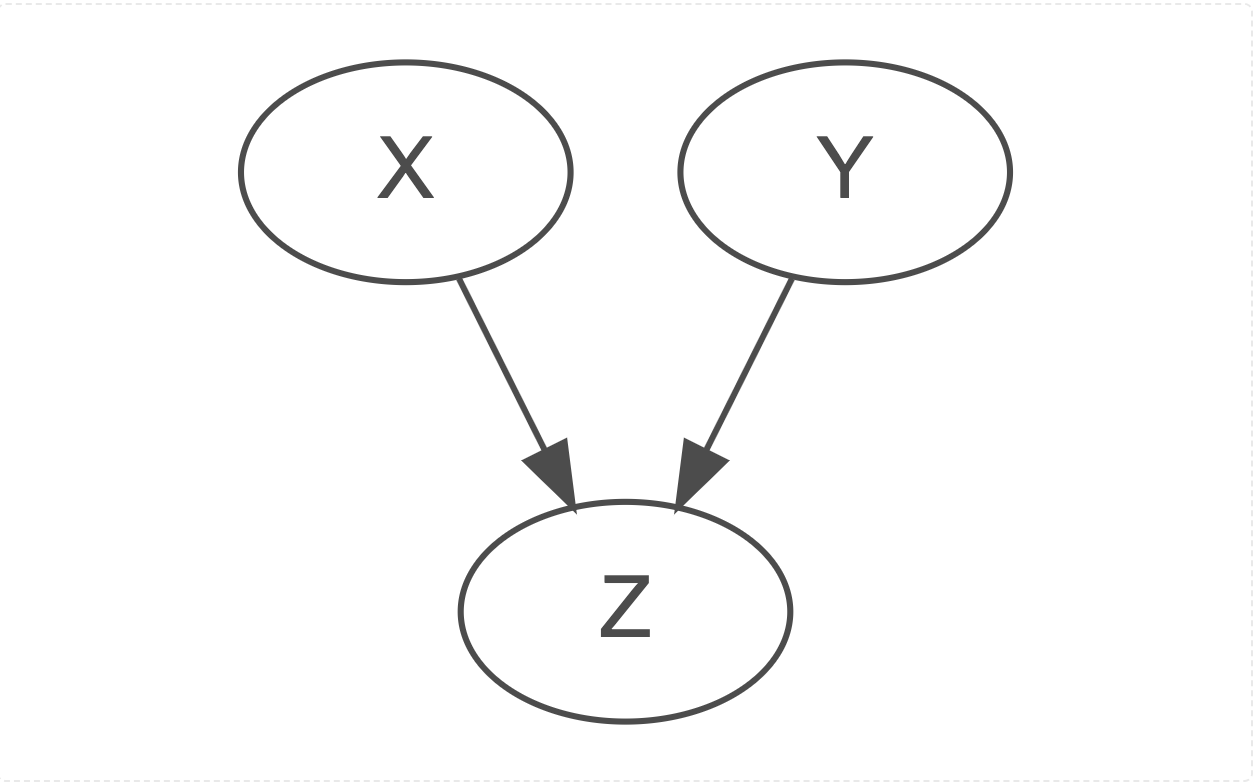
- X and Y below predict Z
- X and Y are completely separate
- X and Y are completely independent of each other
- X and Y are not correlated; they are not co-linear
Here is an alternative way to show an independence between the two predictors:
- Again, X and Y both predict Z
- X may be showing a stronger predictive relationship with Z, here (look at the overlap with Z compared to that between Y and Z)
- And again, X and Y are completely separate
- X and Y are completely independent of each other
- They are not co-linear.
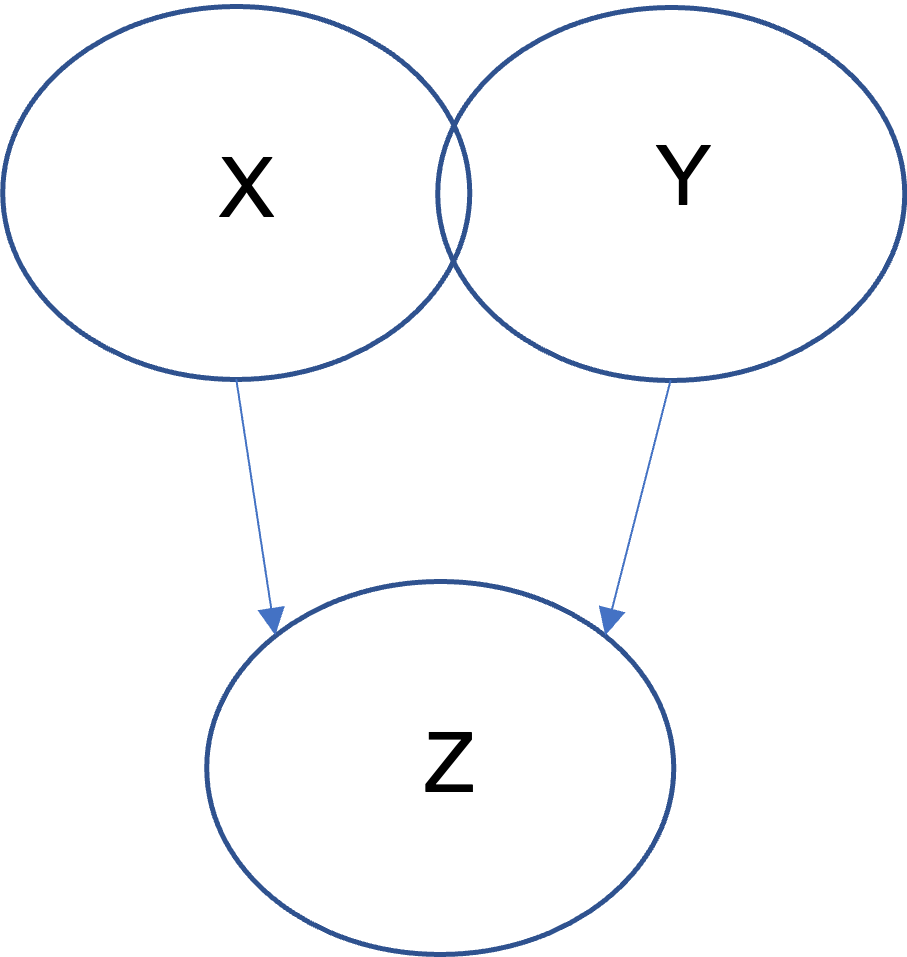
Sometimes the relationship between two predictors is not so independent:
Here X and Y still predict Z, however now they are also correlated with each other, as described by the overlapping areas between X and Y. They share some information. They can be said to be co-linear (very weakly here), as well as being correlated or predicting Z.
We can draw the above diagram this way too…
In this next diagram, the overlap between X and Y is now related to the overlap with Z to a much greater degree…however the correlation between the two predictors of X and Y remains weak.
Multicollinearity
Weak correlations between predictor variables are not too problematic. If predictor variables share strong correlational relationships (normally r > .8), however, the algorithm that is doing the regression calculations for us (behind the scenes) will get a bit mixed up as it will not be able to to tell which predictor is predicting which bit of variance in the outcome variable. Predictors that share strong correlational relationships are fighting for the same part of the variance on Z.
Such strong correlational relationships between predictor variables are known as the predictor set having a high level of multicollinearity. Multicollinearity is likely to occur more in multiple regression simply because there are multiple predictor variables. This is one reason why it is a good idea to do a visualisation of the predictor variables in a correlation matrix, to see, at an early stage in an analysis, if multicollinearity is present. If it is, there are steps to mitigate its effect.
Mitigation
One way to mitigate multicollinearity is to simply leave some variables out of your dataset. There are estimation practices and methods that allow you to choose which to leave out in a principled, reproducible way.
Another way to mitigate multicollinearity is not to discard observed variables but to combine observed variables that are highly correlated together into one new latent variable. This is what a factor analysis method does. It calculates, across a set of otherwise correlated observed variables, what information is unique in a predictor for a hypothesised new variable and takes only sufficient information from each observed variables that uniquely contributes to the new variable. In this way, the multicollinearity amongst the observed variables is reduced with the relevant information from the observed variables retained and described by the new latent variables.
Theory should suggest which variables are likely to “load” together onto a latent variable. When this happens, you may engage in a “confirmatory factor analysis” or CFA. However, you can also take a data driven approach (by letting the model suggest loadings) if theory is agnostic, or variables are quite new. This is sometimes called an “exploratory factor analysis” or EFA.